Quantum-Classical Hybrid Neural Network Comparison
This notebook compares different neural network architectures including:
Classical Multi-Layer Perceptrons (MLP)
Quantum circuits with LINEAR output mapping
Quantum circuits with various GROUPING strategies
1. Import Required Libraries
First, we’ll import all necessary libraries for our experiment:
PyTorch: For neural network implementation and training
Perceval: For quantum circuit simulation
Matplotlib/Seaborn: For visualization
Custom modules: For quantum layers and MLP models
[2]:
from collections import defaultdict
import matplotlib.pyplot as plt
import perceval as pcvl
import seaborn as sns
import torch
import torch.nn as nn
from sklearn.metrics import accuracy_score, classification_report, confusion_matrix
from tqdm import tqdm
import matplotlib
%matplotlib inline
from merlin.core.layer import QuantumLayer, OutputMappingStrategy
from merlin.datasets.mlp_model import MLP, MLPConfig
from merlin.datasets import iris
p ## 2. Load and Prepare the Iris Dataset
We’ll use the classic Iris dataset for multi-class classification. This dataset is ideal for comparing different architectures as it provides a simple but non-trivial classification task.
The dataset contains:
4 features: sepal length, sepal width, petal length, petal width
3 classes: Setosa, Versicolor, Virginica
150 samples total (split into train/test sets)
[3]:
train_features, train_labels, train_metadata = iris.get_data_train()
test_features, test_labels, test_metadata = iris.get_data_test()
# Convert data to PyTorch tensors
X_train = torch.FloatTensor(train_features)
y_train = torch.LongTensor(train_labels)
X_test = torch.FloatTensor(test_features)
y_test = torch.LongTensor(test_labels)
print(f"Training samples: {X_train.shape[0]}")
print(f"Test samples: {X_test.shape[0]}")
print(f"Features: {X_train.shape[1]}")
print(f"Classes: {len(torch.unique(y_train))}")
Training samples: 120
Test samples: 30
Features: 4
Classes: 3
## 3. Define Model Variants
We’ll test several model architectures to compare classical and quantum approaches:
Classical Models:
MLP: Multi-layer perceptron with 8 hidden units, ReLU activation, and 0.1 dropout
Quantum Models:
LINEAR-7modes-nobunching: Uses linear output mapping with 7 quantum modes and no-bunching constraintLEXGROUPING-7modes: Uses lexicographic grouping strategy for output mappingMODGROUPING-7modes: Uses modular grouping strategy for output mapping
Each model type has a distinct color and line style for visualization.
[4]:
def get_model_variants():
"""Define different variants for each model type"""
# Define consistent colors for each model type
MODEL_COLORS = {
'MLP': '#1f77b4', # Blue
'LINEAR': '#2ca02c', # Green
'GROUPING': '#ff7f0e' # Orange
}
# Define line styles for variants
LINE_STYLES = ['--', '-', ':', '-.']
variants = {
'MLP': [
{
'name': 'MLP',
'config': MLPConfig(hidden_sizes=[8], dropout=0.1, activation='relu'),
'color': MODEL_COLORS['MLP'],
'linestyle': LINE_STYLES[0]
}
],
'LINEAR': [
{
'name': 'LINEAR-7modes-nobunching',
'config': {
'm': 7,
'output_mapping_strategy': OutputMappingStrategy.LINEAR,
'no_bunching': True
},
'color': MODEL_COLORS['LINEAR'],
'linestyle': LINE_STYLES[1]
}
],
'GROUPING': [
{
'name': 'LEXGROUPING-7modes',
'config': {
'm': 6,
'output_mapping_strategy': OutputMappingStrategy.LEXGROUPING
},
'color': MODEL_COLORS['GROUPING'],
'linestyle': LINE_STYLES[2]
},
{
'name': 'MODGROUPING-7modes',
'config': {
'm': 6,
'output_mapping_strategy': OutputMappingStrategy.MODGROUPING
},
'color': MODEL_COLORS['GROUPING'],
'linestyle': LINE_STYLES[1]
}
]
}
return variants
## 4. Quantum Circuit Architecture
The quantum circuit is composed of three main sections:
Left interferometer (WL): Performs initial quantum state transformation using beam splitters and phase shifters
Variable phase shifters: Encodes the 4 input features into quantum phases
Right interferometer (WR): Performs final quantum state transformation
The interferometers use a rectangular arrangement of optical elements, where each layer consists of beam splitters (BS) and programmable phase shifters (PS). The phase shifters contain trainable parameters that are optimized during training.
[5]:
def create_quantum_circuit(m):
"""Create quantum circuit with specified number of modes
Parameters:
-----------
m : int
Number of quantum modes in the circuit
Returns:
--------
pcvl.Circuit
Complete quantum circuit with trainable parameters
"""
# Left interferometer with trainable parameters
wl = pcvl.GenericInterferometer(m,
lambda i: pcvl.BS() // pcvl.PS(pcvl.P(f"theta_li{i}")) // \
pcvl.BS() // pcvl.PS(pcvl.P(f"theta_lo{i}")),
shape=pcvl.InterferometerShape.RECTANGLE)
# Variable phase shifters for input encoding
c_var = pcvl.Circuit(m)
for i in range(4): # 4 input features
px = pcvl.P(f"px{i + 1}")
c_var.add(i + (m - 4) // 2, pcvl.PS(px))
# Right interferometer with trainable parameters
wr = pcvl.GenericInterferometer(m,
lambda i: pcvl.BS() // pcvl.PS(pcvl.P(f"theta_ri{i}")) // \
pcvl.BS() // pcvl.PS(pcvl.P(f"theta_ro{i}")),
shape=pcvl.InterferometerShape.RECTANGLE)
# Combine all components
c = pcvl.Circuit(m)
c.add(0, wl, merge=True)
c.add(0, c_var, merge=True)
c.add(0, wr, merge=True)
return c
## 5. Model Factory Functions
These utility functions handle model creation and parameter counting. The create_model function serves as a factory that instantiates either classical MLP models or quantum models based on the specified configuration.
[6]:
def create_model(model_type, variant):
"""Create model instance based on type and variant
Parameters:
-----------
model_type : str
Type of model ('MLP' or quantum model types)
variant : dict
Configuration dictionary for the model variant
Returns:
--------
nn.Module
PyTorch model instance
"""
if model_type == 'MLP':
return MLP(input_size=4, output_size=3, config=variant['config'])
else:
m = variant['config']['m']
no_bunching = variant['config'].get('no_bunching', False)
c = create_quantum_circuit(m)
return QuantumLayer(
input_size=4, output_size=3,
circuit=c,
trainable_parameters=["theta"],
input_parameters=["px"],
input_state=[1, 0] * (m // 2) + [0] * (m % 2),
no_bunching=no_bunching,
output_mapping_strategy=variant['config']['output_mapping_strategy']
)
def count_parameters(model):
"""Count trainable parameters in a PyTorch model"""
return sum(p.numel() for p in model.parameters() if p.requires_grad)
## 6. Training Function
The training function implements a standard supervised learning loop with the following characteristics:
Optimizer: Adam with learning rate 0.02
Loss function: Cross-entropy for multi-class classification
Batch size: 32 samples
Epochs: 50 (default)
The function tracks training loss, training accuracy, and test accuracy at each epoch. After training completes, it generates a detailed classification report.
[7]:
def train_model(model, X_train, y_train, X_test, y_test, model_name, n_epochs=50, batch_size=32, lr=0.02):
"""Train a model and track metrics
Parameters:
-----------
model : nn.Module
Model to train
X_train, y_train : torch.Tensor
Training data and labels
X_test, y_test : torch.Tensor
Test data and labels
model_name : str
Name for progress bar display
n_epochs : int
Number of training epochs
batch_size : int
Batch size for mini-batch training
lr : float
Learning rate
Returns:
--------
dict
Training results including losses, accuracies, and final report
"""
optimizer = torch.optim.Adam(model.parameters(), lr=lr)
criterion = nn.CrossEntropyLoss()
losses = []
train_accuracies = []
test_accuracies = []
model.train()
pbar = tqdm(range(n_epochs), leave=False, desc=f"Training {model_name}")
for epoch in pbar:
# Shuffle training data
permutation = torch.randperm(X_train.size()[0])
total_loss = 0
# Mini-batch training
for i in range(0, X_train.size()[0], batch_size):
indices = permutation[i:i + batch_size]
batch_x, batch_y = X_train[indices], y_train[indices]
outputs = model(batch_x)
loss = criterion(outputs, batch_y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
total_loss += loss.item()
avg_loss = total_loss / (X_train.size()[0] // batch_size)
losses.append(avg_loss)
pbar.set_description(f"Training {model_name} - Loss: {avg_loss:.4f}")
# Evaluation
model.eval()
with torch.no_grad():
# Training accuracy
train_outputs = model(X_train)
train_preds = torch.argmax(train_outputs, dim=1).numpy()
train_acc = accuracy_score(y_train.numpy(), train_preds)
train_accuracies.append(train_acc)
# Test accuracy
test_outputs = model(X_test)
test_preds = torch.argmax(test_outputs, dim=1).numpy()
test_acc = accuracy_score(y_test.numpy(), test_preds)
test_accuracies.append(test_acc)
model.train()
# Generate final classification report
model.eval()
with torch.no_grad():
final_test_outputs = model(X_test)
final_test_preds = torch.argmax(final_test_outputs, dim=1).numpy()
final_report = classification_report(y_test.numpy(), final_test_preds)
return {
'losses': losses,
'train_accuracies': train_accuracies,
'test_accuracies': test_accuracies,
'final_test_acc': test_accuracies[-1],
'classification_report': final_report
}
## 7. Multi-Run Training Function
To ensure robust and statistically meaningful results, we train each model variant multiple times with different random initializations. This approach helps us:
Understand the variance in model performance
Identify which architectures are more stable
Avoid drawing conclusions from lucky/unlucky single runs
Calculate confidence intervals for performance metrics
The function tracks both individual run results and aggregate statistics across all runs.
[8]:
def train_all_variants(X_train, y_train, X_test, y_test, num_runs=5):
"""Train all model variants multiple times and return results
Parameters:
-----------
X_train, y_train : torch.Tensor
Training data and labels
X_test, y_test : torch.Tensor
Test data and labels
num_runs : int
Number of independent training runs per variant
Returns:
--------
tuple
(all_results, best_models) - Complete results and best performing models
"""
variants = get_model_variants()
all_results = defaultdict(dict)
best_models = {}
for model_type, model_variants in variants.items():
print(f"\n\nTraining {model_type} variants:")
best_acc = 0
for variant in model_variants:
print(f"\nTraining {variant['name']}... ({count_parameters(create_model(model_type, variant))} parameters)")
# Store results from multiple runs
variant_runs = []
for run in range(num_runs):
model = create_model(model_type, variant)
print(f" Run {run + 1}/{num_runs}...")
results = train_model(model, X_train, y_train, X_test, y_test, f"{variant['name']}-run{run + 1}")
results['model'] = model
results['color'] = variant['color']
results['linestyle'] = variant['linestyle']
variant_runs.append(results)
# Track best model for each type
if results['final_test_acc'] > best_acc:
best_acc = results['final_test_acc']
best_models[model_type] = {
'name': variant['name'],
'model': model,
'results': results
}
# Store all runs for this variant
all_results[model_type][variant['name']] = {
'runs': variant_runs,
'color': variant['color'],
'linestyle': variant['linestyle'],
'avg_final_test_acc': sum(run['final_test_acc'] for run in variant_runs) / num_runs
}
return all_results, best_models
## 8. Visualization Functions
### Training Curves Visualization
This function creates a comprehensive view of the training process by plotting three key metrics:
Training Loss: Shows how well the model fits the training data
Training Accuracy: Indicates the model’s performance on training samples
Test Accuracy: Reveals the model’s generalization capability
For each model variant, we display:
Solid line: Mean performance across all runs
Shaded area: Performance envelope (min to max values)
This visualization helps identify overfitting, convergence speed, and stability.
[9]:
def plot_training_curves(all_results):
"""Plot training curves for all model variants with average and envelope
Shows three subplots:
1. Training loss over epochs
2. Training accuracy over epochs
3. Test accuracy over epochs
Each line represents the mean across runs, with shaded areas showing min/max envelope.
"""
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(20, 5))
# Plot each metric
for model_type, variants in all_results.items():
for variant_name, variant_data in variants.items():
color = variant_data['color']
linestyle = variant_data['linestyle']
label = f"{variant_name}"
# Get data from all runs
losses_runs = [run['losses'] for run in variant_data['runs']]
train_acc_runs = [run['train_accuracies'] for run in variant_data['runs']]
test_acc_runs = [run['test_accuracies'] for run in variant_data['runs']]
# Calculate mean values across all runs
epochs = len(losses_runs[0])
mean_losses = [sum(run[i] for run in losses_runs) / len(losses_runs) for i in range(epochs)]
mean_train_acc = [sum(run[i] for run in train_acc_runs) / len(train_acc_runs) for i in range(epochs)]
mean_test_acc = [sum(run[i] for run in test_acc_runs) / len(test_acc_runs) for i in range(epochs)]
# Calculate min and max values for the envelope
min_losses = [min(run[i] for run in losses_runs) for i in range(epochs)]
max_losses = [max(run[i] for run in losses_runs) for i in range(epochs)]
min_train_acc = [min(run[i] for run in train_acc_runs) for i in range(epochs)]
max_train_acc = [max(run[i] for run in train_acc_runs) for i in range(epochs)]
min_test_acc = [min(run[i] for run in test_acc_runs) for i in range(epochs)]
max_test_acc = [max(run[i] for run in test_acc_runs) for i in range(epochs)]
# Plot mean lines
ax1.plot(mean_losses, label=label, color=color, linestyle=linestyle, linewidth=2)
ax2.plot(mean_train_acc, label=label, color=color, linestyle=linestyle, linewidth=2)
ax3.plot(mean_test_acc, label=label, color=color, linestyle=linestyle, linewidth=2)
# Plot envelopes (filled area between min and max)
epochs_range = range(epochs)
ax1.fill_between(epochs_range, min_losses, max_losses, color=color, alpha=0.2)
ax2.fill_between(epochs_range, min_train_acc, max_train_acc, color=color, alpha=0.2)
ax3.fill_between(epochs_range, min_test_acc, max_test_acc, color=color, alpha=0.2)
# Customize plots
for ax, title in zip([ax1, ax2, ax3], ['Training Loss', 'Training Accuracy', 'Test Accuracy']):
ax.set_title(title, fontsize=12, pad=10)
ax.set_xlabel('Epoch', fontsize=10)
ax.set_ylabel(title.split()[-1], fontsize=10)
ax.legend(fontsize=8, bbox_to_anchor=(1.05, 1), loc='upper left')
ax.grid(True, linestyle='--', alpha=0.7)
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
plt.tight_layout()
plt.show()
### Confusion Matrix Visualization
Confusion matrices provide detailed insights into classification performance by showing:
Which classes are correctly classified (diagonal elements)
Which classes are confused with each other (off-diagonal elements)
Overall performance patterns for each model architecture
We display the confusion matrix for the best-performing model of each type.
[10]:
def plot_best_confusion_matrices(best_models, X_test, y_test):
"""Plot confusion matrices for the best model of each type"""
fig, axes = plt.subplots(1, 3, figsize=(20, 5))
class_names = ['setosa', 'versicolor', 'virginica']
for idx, (model_type, best) in enumerate(best_models.items()):
model = best['model']
model.eval()
with torch.no_grad():
outputs = model(X_test)
predictions = torch.argmax(outputs, dim=1).numpy()
cm = confusion_matrix(y_test.numpy(), predictions)
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues',
xticklabels=class_names, yticklabels=class_names, ax=axes[idx])
axes[idx].set_title(f'Best {model_type}\n({best["name"]})')
axes[idx].set_xlabel('Predicted')
axes[idx].set_ylabel('True')
plt.setp(axes[idx].get_xticklabels(), rotation=45)
plt.setp(axes[idx].get_yticklabels(), rotation=45)
plt.tight_layout()
plt.show()
## 9. Results Summary Function
This function provides a comprehensive statistical analysis of the experimental results, including:
Parameter efficiency: Number of trainable parameters for each model
Performance statistics: Mean accuracy, standard deviation, min/max values
Detailed classification reports: Precision, recall, and F1-score for each class
These metrics help in making informed decisions about model selection based on the specific requirements of your application.
[11]:
def print_comparison_results(all_results, best_models):
"""Print detailed comparison of all models and variants with multi-run statistics"""
print("\n----- Model Comparison Results -----")
# Print results for all variants
print("\nAll Model Variants Results (averaged over multiple runs):")
for model_type, variants in all_results.items():
print(f"\n{model_type} Variants:")
for variant_name, variant_data in variants.items():
print(f"\n{variant_name}:")
print(f"Parameters: {count_parameters(variant_data['runs'][0]['model'])}")
# Calculate statistics across runs
final_accs = [run['final_test_acc'] for run in variant_data['runs']]
avg_acc = sum(final_accs) / len(final_accs)
min_acc = min(final_accs)
max_acc = max(final_accs)
std_acc = (sum((acc - avg_acc) ** 2 for acc in final_accs) / len(final_accs)) ** 0.5
print(f"Final Test Accuracy: {avg_acc:.4f} ± {std_acc:.4f} (min: {min_acc:.4f}, max: {max_acc:.4f})")
# Print best model results
print("\nBest Models:")
for model_type, best in best_models.items():
print(f"\nBest {model_type} Model: {best['name']}")
print(f"Final Test Accuracy: {best['results']['final_test_acc']:.4f}")
print(f"Classification Report:\n{best['results']['classification_report']}")
## 10. Run the Complete Experiment
Now we’ll execute the full experimental pipeline. The experiment consists of:
Multiple training runs: Each model variant is trained 5 times with different random seeds
Performance tracking: All metrics are recorded for statistical analysis
Visualization: Training curves and confusion matrices are generated
Statistical summary: Detailed performance statistics are computed
This comprehensive approach ensures reliable and reproducible results.
[12]:
# Set number of independent runs per model variant
num_runs = 5
# Train all variants
print("Starting training process...")
all_results, best_models = train_all_variants(X_train, y_train, X_test, y_test, num_runs=num_runs)
Starting training process...
Training MLP variants:
Training MLP... (67 parameters)
Run 1/5...
Run 2/5...
Run 3/5...
Run 4/5...
Run 5/5...
Training LINEAR variants:
Training LINEAR-7modes-nobunching... (192 parameters)
Run 1/5...
Run 2/5...
Run 3/5...
Run 4/5...
Run 5/5...
Training GROUPING variants:
Training LEXGROUPING-7modes... (60 parameters)
Run 1/5...
Run 2/5...
Run 3/5...
Run 4/5...
/Users/senellart/DEV/merlin_new/venv/lib/python3.13/site-packages/sklearn/metrics/_classification.py:1565: UndefinedMetricWarning: Precision is ill-defined and being set to 0.0 in labels with no predicted samples. Use `zero_division` parameter to control this behavior.
_warn_prf(average, modifier, f"{metric.capitalize()} is", len(result))
/Users/senellart/DEV/merlin_new/venv/lib/python3.13/site-packages/sklearn/metrics/_classification.py:1565: UndefinedMetricWarning: Precision is ill-defined and being set to 0.0 in labels with no predicted samples. Use `zero_division` parameter to control this behavior.
_warn_prf(average, modifier, f"{metric.capitalize()} is", len(result))
/Users/senellart/DEV/merlin_new/venv/lib/python3.13/site-packages/sklearn/metrics/_classification.py:1565: UndefinedMetricWarning: Precision is ill-defined and being set to 0.0 in labels with no predicted samples. Use `zero_division` parameter to control this behavior.
_warn_prf(average, modifier, f"{metric.capitalize()} is", len(result))
Run 5/5...
Training MODGROUPING-7modes... (60 parameters)
Run 1/5...
Run 2/5...
Run 3/5...
/Users/senellart/DEV/merlin_new/venv/lib/python3.13/site-packages/sklearn/metrics/_classification.py:1565: UndefinedMetricWarning: Precision is ill-defined and being set to 0.0 in labels with no predicted samples. Use `zero_division` parameter to control this behavior.
_warn_prf(average, modifier, f"{metric.capitalize()} is", len(result))
/Users/senellart/DEV/merlin_new/venv/lib/python3.13/site-packages/sklearn/metrics/_classification.py:1565: UndefinedMetricWarning: Precision is ill-defined and being set to 0.0 in labels with no predicted samples. Use `zero_division` parameter to control this behavior.
_warn_prf(average, modifier, f"{metric.capitalize()} is", len(result))
/Users/senellart/DEV/merlin_new/venv/lib/python3.13/site-packages/sklearn/metrics/_classification.py:1565: UndefinedMetricWarning: Precision is ill-defined and being set to 0.0 in labels with no predicted samples. Use `zero_division` parameter to control this behavior.
_warn_prf(average, modifier, f"{metric.capitalize()} is", len(result))
Run 4/5...
Run 5/5...
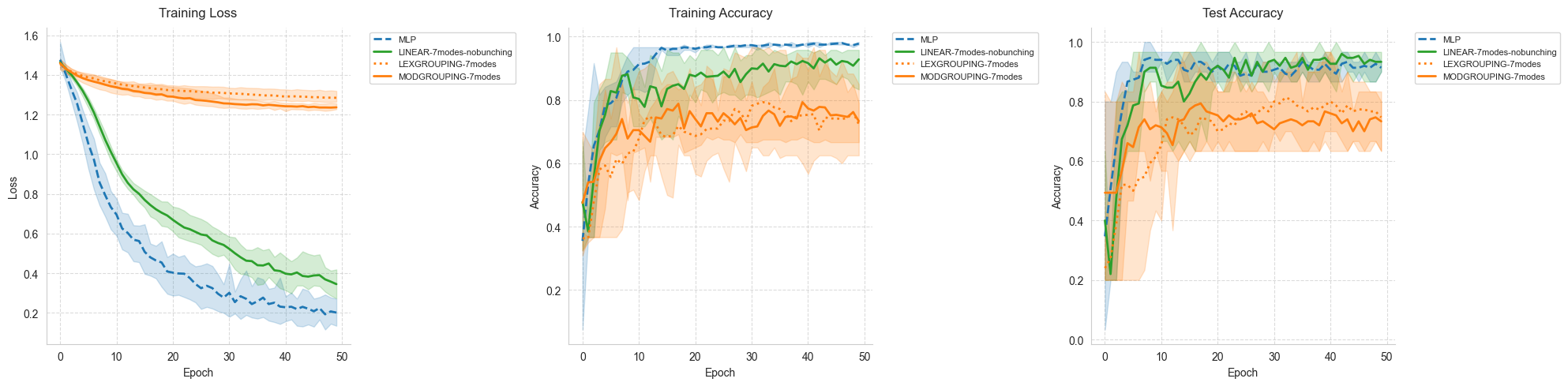
### Visualize Training Progress
The following plots show how each model’s performance evolves during training. Pay attention to:
Convergence speed: How quickly each model reaches its best performance
Stability: Width of the shaded area indicates variance across runs
Final performance: Where each model plateaus
[13]:
plot_training_curves(all_results)
### Confusion Matrices for Best Models
These confusion matrices reveal the classification patterns of the best-performing model from each architecture type. Look for:
Perfect classification: Bright blue diagonal with zeros elsewhere
Common confusions: Off-diagonal elements show which classes are hard to distinguish
[14]:
print_comparison_results(all_results, best_models)
----- Model Comparison Results -----
All Model Variants Results (averaged over multiple runs):
MLP Variants:
MLP:
Parameters: 67
Final Test Accuracy: 0.9133 ± 0.0400 (min: 0.8667, max: 0.9667)
LINEAR Variants:
LINEAR-7modes-nobunching:
Parameters: 192
Final Test Accuracy: 0.9467 ± 0.0267 (min: 0.9000, max: 0.9667)
GROUPING Variants:
LEXGROUPING-7modes:
Parameters: 60
Final Test Accuracy: 0.6800 ± 0.0267 (min: 0.6333, max: 0.7000)
MODGROUPING-7modes:
Parameters: 60
Final Test Accuracy: 0.7000 ± 0.0699 (min: 0.6333, max: 0.8333)
Best Models:
Best MLP Model: MLP
Final Test Accuracy: 0.9667
Classification Report:
precision recall f1-score support
0 1.00 1.00 1.00 13
1 1.00 0.83 0.91 6
2 0.92 1.00 0.96 11
accuracy 0.97 30
macro avg 0.97 0.94 0.96 30
weighted avg 0.97 0.97 0.97 30
Best LINEAR Model: LINEAR-7modes-nobunching
Final Test Accuracy: 0.9667
Classification Report:
precision recall f1-score support
0 1.00 1.00 1.00 13
1 1.00 0.83 0.91 6
2 0.92 1.00 0.96 11
accuracy 0.97 30
macro avg 0.97 0.94 0.96 30
weighted avg 0.97 0.97 0.97 30
Best GROUPING Model: MODGROUPING-7modes
Final Test Accuracy: 0.8333
Classification Report:
precision recall f1-score support
0 1.00 1.00 1.00 13
1 0.55 1.00 0.71 6
2 1.00 0.55 0.71 11
accuracy 0.83 30
macro avg 0.85 0.85 0.80 30
weighted avg 0.91 0.83 0.83 30
## 11. Key Findings and Conclusions
Based on the experimental results, we can draw several important conclusions:
Model Complexity vs Performance:
Compare the number of parameters required by each architecture
Assess whether quantum models achieve similar performance with fewer parameters
Training Stability:
The variance across multiple runs indicates how sensitive each model is to initialization
Lower variance suggests more reliable training
Generalization Capability:
The gap between training and test accuracy reveals overfitting tendencies
Smaller gaps indicate better generalization
Classification Patterns:
Confusion matrices show which flower species are most difficult to distinguish
This can guide feature engineering or model selection
Practical Considerations:
For deployment, consider:
Classical MLPs: Well-understood, fast inference, established deployment pipelines
Quantum models: Potentially more parameter-efficient, may offer advantages on quantum hardware
Future Research Directions:
Scaling to larger datasets: Test on more complex classification tasks
Noise modeling: Investigate performance under realistic quantum noise conditions
Hybrid architectures: Combine classical and quantum layers
Hardware implementation: Evaluate on actual quantum photonic devices
Feature encoding strategies: Explore different ways to encode classical data into quantum states