Expressive power of the variational linear quantum photonic circuit (dependent of photon number)

The goal here will be to fit a degree 3 Fourier series g(x) with a Variational Quantum Circuit (VQC) using MerLin for the optimization. Since this is a fitting task, we won’t use a validation or test dataset because our goal is to overfit on the data to assess the expressivity of a VQC.

As we will see, the expressivity of a VQC depends on the number of photons sent through the quantum circuit.

This notebook presents an experiment from the paper: Fock State-enhanced Expressivity of Quantum Machine Learning Models.

0. Imports and prep

# Import required libraries
import matplotlib.pyplot as plt
import perceval as pcvl
import torch
import torch.nn as nn
import numpy as np
from sklearn.metrics import mean_squared_error
from tqdm import tqdm
from math import comb

# Import from our custom packages
from merlin import QuantumLayer, OutputMappingStrategy

1. Define input domain, x, and target function g(x)

x = np.arange(-3*np.pi, 3*np.pi+0.01, 0.05)

# Fourier coefficents
c_0 = 0.2
c_1 = 0.69 + 0.52j
c_2 = 0.81 + 0.41j
c_3 = 0.68 + 0.82j
# We want real valued g(x) so we have c_{-n} = conjugate( c_{n})
coefs = np.array([np.conj(c_3), np.conj(c_2), np.conj(c_1), c_0, c_1, c_2, c_3])
n = np.arange(-3, 4, 1)

# Compute the Fourier series sum
g = np.zeros_like(x, dtype=complex)
for k, c in zip(n, coefs):
    g += c * np.exp(1j * k * x)

# g should be real valued
assert np.allclose(g, g.real), "g != g.real"
g = g.real

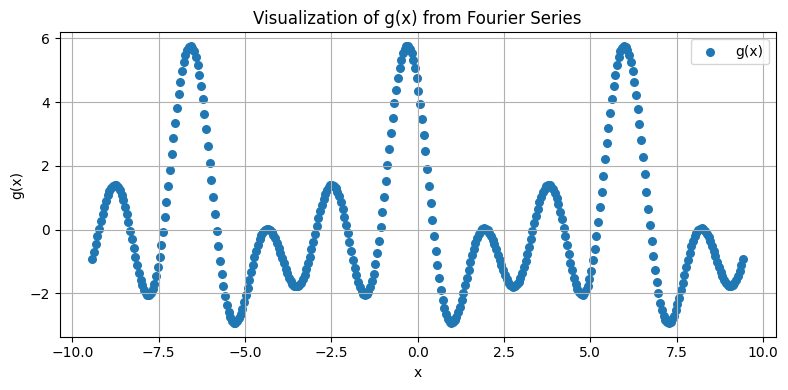
Let’s visualize g(x)

# Plot using matplotlib
plt.figure(figsize=(8, 4))
plt.scatter(x, g, label='g(x)', s=30)
plt.title('Visualization of g(x) from Fourier Series')
plt.xlabel('x')
plt.ylabel('g(x)')
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()
plt.clf()

<Figure size 640x480 with 0 Axes>

2. Model definitions

First off, we define the photonic circuit using Perceval.

def create_vqc_general(m, input_size):
    """Create variational quantum classifier with specified number of modes using general meshes"""

    wl = pcvl.GenericInterferometer(m,
                                    lambda i: pcvl.BS() // pcvl.PS(pcvl.P(f"theta_li{i}_ps")) // \
                                              pcvl.BS() // pcvl.PS(pcvl.P(f"theta_lo{i}_ps")),
                                    shape=pcvl.InterferometerShape.RECTANGLE)

    c_var = pcvl.Circuit(m)
    for i in range(input_size):
        px = pcvl.P(f"px{i + 1}")
        c_var.add(i + (m - input_size) // 2, pcvl.PS(px))

    wr = pcvl.GenericInterferometer(m,
                                    lambda i: pcvl.BS() // pcvl.PS(pcvl.P(f"theta_ri{i}_ps")) // \
                                              pcvl.BS() // pcvl.PS(pcvl.P(f"theta_ro{i}_ps")),
                                    shape=pcvl.InterferometerShape.RECTANGLE)

    c = pcvl.Circuit(m)
    c.add(0, wl, merge=True)
    c.add(0, c_var, merge=True)
    c.add(0, wr, merge=True)

    return c

def count_parameters(model):
    """Count trainable parameters in a PyTorch model"""
    return sum(p.numel() for p in model.parameters() if p.requires_grad)

example_circuit = create_vqc_general(3, 1)
pcvl.pdisplay(example_circuit)

We will define a scaling layer for the first layer of our model. It simply multiplies the input by a constant.

class ScaleLayer(nn.Module):
    """
        Multiply the input tensor by a learned or fixed factor.

        Args:
            dim (int): Dimension of the input data to be encoded.
            scale_type (str): Type of scaling method.

        Returns: nn.Module that multiplies the input tensor by a learned or fixed factor.
    """
    def __init__(self, dim, scale_type = "learned"):
        super(ScaleLayer, self).__init__()
        # Create a single learnable parameter (initialized to 1.0 by default)
        if scale_type == "learned":
            self.scale = nn.Parameter(torch.rand(dim))
        elif scale_type == "2pi":
            self.scale = torch.full((dim,), 2 * torch.pi)
        elif scale_type == "/2pi":
            self.scale = torch.full((dim,), 1/ (2 * torch.pi))
        elif scale_type == "/2":
            self.scale = torch.full((dim,), 1/ 2)
        elif scale_type == "pi":
            self.scale = torch.full((dim,), torch.pi)
        elif scale_type == "/pi":
            self.scale = torch.full((dim,), 1 / torch.pi)
        elif scale_type == "1":
            self.scale = torch.full((dim,), 1)

    def forward(self, x):
        # Element-wise multiplication of each input element by the learned scale
        return x * self.scale

Then, we use MerLin’s QuantumLayer which allows backpropagation for optimization with gradient descent. It was also designed to be used with PyTorch so this facilitates its usage immensely.

Let’s create three quantum layers that each have a different input state to their circuit. Then, let’s see how this affects their number of parameters.

def create_quantum_layer(initial_state):
    """ Create a quantum layer consisting of a VQC for a specific initial state """

    vqc = QuantumLayer(
                input_size=1,
                output_size=1,
                circuit=create_vqc_general(3, 1),
                trainable_parameters=["theta"],
                input_parameters=["px"],
                input_state= initial_state,
                no_bunching=False,
                output_mapping_strategy=OutputMappingStrategy.LINEAR,
            )

    return vqc


def create_model(initial_state):
    scale_layer = ScaleLayer(1, scale_type = "/pi")
    vqc = create_quantum_layer(initial_state)

    return nn.Sequential(scale_layer, vqc)

vqc_100 = create_model([1, 0, 0])
vqc_110 = create_model([1, 1, 0])
vqc_111 = create_model([1, 1, 1])

models = {"VQC_[1, 0, 0]" : vqc_100, "VQC_[1, 1, 0]" : vqc_110, "VQC_[1, 1, 1]" : vqc_111}

for name, model in models.items():
    print(f"{name}: {count_parameters(model)} parameters")

VQC_[1, 0, 0]: 16 parameters
VQC_[1, 1, 0]: 19 parameters
VQC_[1, 1, 1]: 23 parameters

3. Training function

The optimization for the quantum model is as easy as for a classical PyTorch model thanks to MerLin. The structure of the training loop remains the same !

Note that the loss function used for training is the Mean Squared Error (MSE) loss which is useful for regression tasks.

def train_model(model, X_train, y_train, model_name, n_epochs=60, batch_size=32, lr=0.02, betas=[0.9, 0.999]):
    """Train a model and return training metrics"""
    optimizer = torch.optim.Adam(model.parameters(), lr=lr, betas=betas)
    criterion = nn.MSELoss()

    losses = []
    train_mses = []

    model.train()

    pbar = tqdm(range(n_epochs), desc=f"Training {model_name}")
    for epoch in pbar:
        permutation = torch.randperm(X_train.size()[0])
        total_loss = 0

        for i in range(0, X_train.size()[0], batch_size):
            indices = permutation[i:i + batch_size]
            batch_x, batch_y = X_train[indices], y_train[indices]

            outputs = model(batch_x)
            loss = criterion(outputs.squeeze(), batch_y.squeeze())

            optimizer.zero_grad()
            loss.backward()
            optimizer.step()

            total_loss += loss.item()

        avg_loss = total_loss / (X_train.size()[0] // batch_size)
        losses.append(avg_loss)

        # Evaluation
        model.eval()
        with torch.no_grad():
            train_outputs = model(X_train)
            train_mse = mean_squared_error(y_train.numpy(), train_outputs)
            train_mses.append(train_mse)

            pbar.set_description(f"Training {model_name} - Loss: {avg_loss:.4f}, Train MSE: {train_mse:.4f}")

        model.train()

    return {
        'losses': losses,
        'train_mses': train_mses,
    }

def train_models_multiple_runs(initial_states, colors, X_train, y_train, num_runs=5):
    """Train all models multiple times and return results"""
    results = {}
    models = []

    for initial_state, color in zip(initial_states, colors):
        print(f"\nTraining VQC with initial state: {initial_state} ({num_runs} runs):")
        pending_models = []
        model_runs = []

        for run in range(num_runs):
            # Create a fresh instance of the model for each run
            vqc = create_model(initial_state)

            print(f"  Run {run+1}/{num_runs}...")
            run_results = train_model(vqc, torch.tensor(X_train, dtype=torch.float).unsqueeze(-1), torch.tensor(y_train, dtype=torch.float), f"VQC_{initial_state}-run{run+1}")
            pending_models.append(vqc)
            model_runs.append(run_results)

        # Find and keep the best model for each initial state
        index = torch.argmin(torch.tensor([model_run["train_mses"][-1] for model_run in model_runs]))

        models.append(pending_models[index])
        # Store all runs for this model
        results[f"VQC_{initial_state}"] = {
            "runs": model_runs,
            "color": color,
        }

    return results, models

# Define number of runs per model
num_runs = 3

initial_states = [[1, 0, 0], [1, 1, 0], [1, 1, 1]]

colors = ["blue", "orange", "red"]

# Train all models
all_results, models = train_models_multiple_runs(initial_states, colors, x, g, num_runs=num_runs)

Training VQC with initial state: [1, 0, 0] (3 runs):
  Run 1/3...

Training VQC_[1, 0, 0]-run1 - Loss: 4.2597, Train MSE: 3.9085: 100%|██████████| 60/60 [00:04<00:00, 13.75it/s]

  Run 2/3...

Training VQC_[1, 0, 0]-run2 - Loss: 4.2933, Train MSE: 3.9207: 100%|██████████| 60/60 [00:03<00:00, 15.06it/s]

  Run 3/3...

Training VQC_[1, 0, 0]-run3 - Loss: 4.2789, Train MSE: 3.9123: 100%|██████████| 60/60 [00:04<00:00, 13.87it/s]

Training VQC with initial state: [1, 1, 0] (3 runs):
  Run 1/3...

Training VQC_[1, 1, 0]-run1 - Loss: 2.4816, Train MSE: 2.2958: 100%|██████████| 60/60 [00:04<00:00, 12.59it/s]

  Run 2/3...

Training VQC_[1, 1, 0]-run2 - Loss: 2.5101, Train MSE: 2.2692: 100%|██████████| 60/60 [00:04<00:00, 12.16it/s]

  Run 3/3...

Training VQC_[1, 1, 0]-run3 - Loss: 2.4925, Train MSE: 2.2723: 100%|██████████| 60/60 [00:04<00:00, 12.22it/s]

Training VQC with initial state: [1, 1, 1] (3 runs):
  Run 1/3...

Training VQC_[1, 1, 1]-run1 - Loss: 0.0100, Train MSE: 0.0089: 100%|██████████| 60/60 [00:05<00:00, 11.62it/s]

  Run 2/3...

Training VQC_[1, 1, 1]-run2 - Loss: 0.0000, Train MSE: 0.0000: 100%|██████████| 60/60 [00:05<00:00, 10.95it/s]

  Run 3/3...

Training VQC_[1, 1, 1]-run3 - Loss: 0.0053, Train MSE: 0.0044: 100%|██████████| 60/60 [00:05<00:00, 11.97it/s]

4. Plot training loss

def plot_training_curves(all_results):
    """Plot training curves for all model variants with average and envelope (only loss shown)"""
    fig, ax = plt.subplots(1, 1, figsize=(10, 6))

    # Plot each metric
    for model_name, model_data in all_results.items():
        color = model_data['color']
        linestyle = '-'

        # Get data from all runs
        losses_runs = [run['losses'] for run in model_data['runs']]

        # Calculate mean values across all runs
        epochs = len(losses_runs[0])
        mean_losses = [sum(run[i] for run in losses_runs) / len(losses_runs) for i in range(epochs)]

        # Calculate min and max values for the envelope
        min_losses = [min(run[i] for run in losses_runs) for i in range(epochs)]
        max_losses = [max(run[i] for run in losses_runs) for i in range(epochs)]

        # Plot mean line
        ax.plot(mean_losses, label=model_name, color=color, linestyle=linestyle, linewidth=2)

        # Plot envelope
        ax.fill_between(range(epochs), min_losses, max_losses, color=color, alpha=0.2)

    # Customize plot
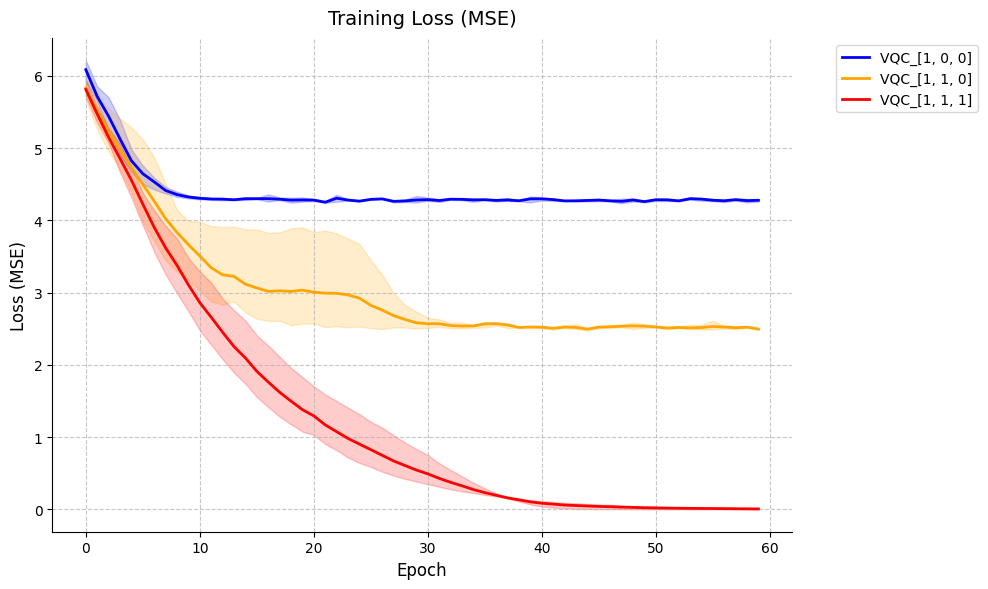
    ax.set_title('Training Loss (MSE)', fontsize=14, pad=10)
    ax.set_xlabel('Epoch', fontsize=12)
    ax.set_ylabel('Loss (MSE)', fontsize=12)
    ax.legend(fontsize=10, bbox_to_anchor=(1.05, 1), loc='upper left')
    ax.grid(True, linestyle='--', alpha=0.7)
    ax.spines['top'].set_visible(False)
    ax.spines['right'].set_visible(False)

    plt.tight_layout()
    # plt.savefig("./results/expressive_power_vqc_loss.png")
    plt.show()
    plt.clf()


# Plot training curves
plot_training_curves(all_results)

<Figure size 640x480 with 0 Axes>

5. Summary of results

def print_summary_statistics(all_results):
    """Print summary statistics for all models"""
    print("\n----- Model Comparison Results -----\n")

    for model_name, model_data in all_results.items():
        # Calculate statistics across runs
        final_mses = [run['train_mses'][-1] for run in model_data['runs']]
        avg_mse = sum(final_mses) / len(final_mses)
        min_mse = min(final_mses)
        max_mse = max(final_mses)
        std_mse = (sum((mse - avg_mse) ** 2 for mse in final_mses) / len(final_mses)) ** 0.5

        print(f"{model_name}:")
        print(f"  Final train MSE: {avg_mse:.6f} ± {std_mse:.6f} (min: {min_mse:.6f}, max: {max_mse:.6f})")
        print()

# Print summary statistics
print_summary_statistics(all_results)

----- Model Comparison Results -----

VQC_[1, 0, 0]:
  Final train MSE: 3.913869 ± 0.005102 (min: 3.908540, max: 3.920746)

VQC_[1, 1, 0]:
  Final train MSE: 2.279082 ± 0.011891 (min: 2.269184, max: 2.295804)

VQC_[1, 1, 1]:
  Final train MSE: 0.004431 ± 0.003619 (min: 0.000000, max: 0.008866)

6. Visualize learned functions

def visualize_learned_function(models, names, colors, x, g):
    """Visualize learned function of different models to compare them with the target function, g(x)"""
    # Plot using matplotlib
    plt.figure(figsize=(8, 4))
    plt.scatter(x, g, label='g(x)', s=30)

    for model, name, color in zip(models, names, colors):
        model.eval()
        with torch.no_grad():
            output = model(torch.tensor(x, dtype=torch.float).unsqueeze(-1))
        plt.plot(x, output.detach().numpy(), label=name, color=color, linewidth=3)

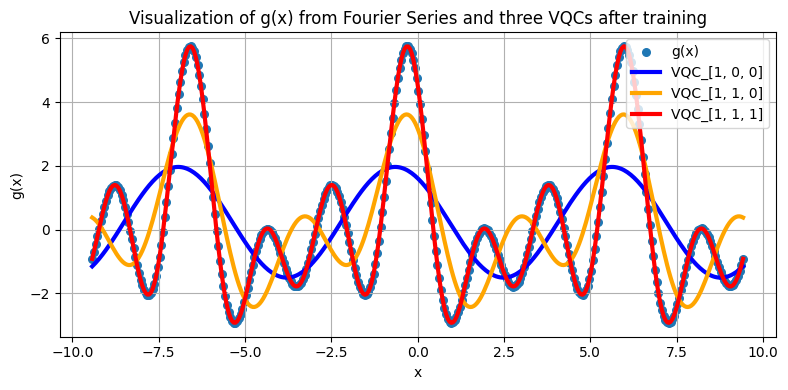
    plt.title('Visualization of g(x) from Fourier Series and three VQCs after training')
    plt.xlabel('x')
    plt.ylabel('g(x)')
    plt.grid(True)
    plt.legend()
    plt.tight_layout()
    # plt.savefig("./results/expressive_power_of_the_VQC.png")  # To save the figure locally
    plt.show()
    plt.clf()
    return

names = ["VQC_[1, 0, 0]", "VQC_[1, 1, 0]", "VQC_[1, 1, 1]"]
colors = ["blue", "orange", "red"]
visualize_learned_function(models, names, colors, x, g)

<Figure size 640x480 with 0 Axes>

Hence, this result demonstrates that a quantum model with more input photons can be more expressive. This paper explains this phenomena by the fact that quantum models with more input photons have access to more basis functions, so they can learn Fourier series with higher frequencies.