merlin.algorithms.layer module

Main QuantumLayer implementation

class merlin.algorithms.layer.Any(*args, **kwargs)

Bases: object

Special type indicating an unconstrained type.

• Any is compatible with every type.

• Any assumed to have all methods.

• All values assumed to be instances of Any.

Note that all the above statements are true from the point of view of static type checkers. At runtime, Any should not be used with instance checks.

class merlin.algorithms.layer.AutoDiffProcess(sampling_method='multinomial')

Bases: object

Handles automatic differentiation backend and sampling noise integration.

autodiff_backend(needs_gradient, apply_sampling, shots)

Determine sampling configuration based on gradient requirements.

Return type:

tuple[bool, int]

class merlin.algorithms.layer.CircuitBuilder(n_modes)

Bases: object

Builder for quantum circuits using a declarative API.

add_angle_encoding(modes=None, name=None, *, scale=1.0, subset_combinations=False, max_order=None)

Convenience method for angle-based input encoding.

Return type:

CircuitBuilder

Args:

modes: Optional list of circuit modes to target. Defaults to all modes. name: Prefix used for generated input parameters. Defaults to "px". scale: Global scaling factor applied before angle mapping. subset_combinations: When True, generate higher-order feature

combinations (up to max_order) similar to the legacy FeatureEncoder.

max_order: Optional cap on the size of feature combinations when

subset_combinations is enabled. None uses all orders.

Returns:

CircuitBuilder: self for fluent chaining.

add_entangling_layer(modes=None, *, trainable=True, model='mzi', name=None, trainable_inner=None, trainable_outer=None)

Add an entangling layer spanning a range of modes.

Return type:

CircuitBuilder

Args:

modes: Optional list describing the span. None targets all modes;

one element targets modes[0] through the final mode; two elements target the inclusive range [modes[0], modes[1]].

trainable: Whether internal phase shifters should be trainable. model: "mzi" or "bell" to select the internal interferometer template. name: Optional prefix used for generated parameter names. trainable_inner: Override for the internal (between-beam splitter) phase shifters. trainable_outer: Override for the output phase shifters at the exit of the interferometer.

Raises:

ValueError: If the provided modes are invalid or span fewer than two modes.

Returns:

CircuitBuilder: self for fluent chaining.

add_rotations(modes=None, *, axis='z', trainable=False, as_input=False, angle=None, value=None, name=None, role=None)

Add one or multiple rotations across the provided modes.

Return type:

CircuitBuilder

Args:

modes: Single mode, list of modes, module group or None (all modes). axis: Axis of rotation for each inserted phase shifter. trainable: Promote the rotations to trainable parameters (legacy flag). as_input: Mark the rotations as input-driven parameters (legacy flag). angle: Optional fixed value for the rotations (alias of value). value: Optional fixed value for the rotations (alias of angle). name: Optional stem used for generated parameter names. role: Explicit ParameterRole taking precedence over other flags.

Returns:

CircuitBuilder: self for fluent chaining.

add_superpositions(targets=None, *, depth=1, theta=0.785398, phi=0.0, trainable=None, trainable_theta=None, trainable_phi=None, modes=None, name=None)

Add one or more superposition (beam splitter) components.

Return type:

CircuitBuilder

Args:

targets: Tuple or list of tuples describing explicit mode pairs. When

omitted, nearest neighbours over modes (or all modes) are used.

depth: Number of sequential passes to apply (>=1). theta: Baseline mixing angle for fixed beam splitters. phi: Baseline relative phase for fixed beam splitters. trainable: Convenience flag to mark both theta and phi trainable. trainable_theta: Whether the mixing angle should be trainable. trainable_phi: Whether the relative phase should be trainable. modes: Optional mode list/module group used when targets is omitted. name: Optional stem used for generated parameter names.

Returns:

CircuitBuilder: self for fluent chaining.

property angle_encoding_specs: dict[str, dict[str, Any]]

Return metadata describing configured angle encodings.

Returns:

Dict[str, Dict[str, Any]]: Mapping from encoding prefix to combination metadata.

build()

Build and return the circuit.

Return type:

Circuit

Returns:

Circuit: Circuit instance populated with components.

classmethod from_circuit(circuit)

Create a builder from an existing circuit.

Return type:

CircuitBuilder

Args:

circuit: Circuit object whose components should seed the builder.

Returns:

CircuitBuilder: A new builder instance wrapping the provided circuit.

property input_parameter_prefixes: list[str]

Expose the order-preserving set of input prefixes.

Returns:

List[str]: Input parameter stems emitted during encoding.

to_pcvl_circuit(pcvl_module=None)

Convert the constructed circuit into a Perceval circuit.

Args:

pcvl_module: Optional Perceval module. If None, attempts to import perceval.

Returns:

A pcvl.Circuit instance mirroring the components tracked by this builder.

Raises:

ImportError: If perceval is not installed and no module is provided.

property trainable_parameter_prefixes: list[str]

Expose the unique set of trainable prefixes in insertion order.

Returns:

List[str]: Trainable parameter stems discovered so far.

class merlin.algorithms.layer.ComputationProcessFactory

Bases: object

Factory for creating computation processes.

static create(circuit, input_state, trainable_parameters, input_parameters, reservoir_mode=False, computation_space=None, **kwargs)

Create a computation process.

Return type:

ComputationProcess

enum merlin.algorithms.layer.ComputationSpace(value)

Bases: str, Enum

Enumeration of supported computational subspaces.

Member Type:

str

Valid values are as follows:

FOCK = <ComputationSpace.FOCK: 'fock'>

UNBUNCHED = <ComputationSpace.UNBUNCHED: 'unbunched'>

DUAL_RAIL = <ComputationSpace.DUAL_RAIL: 'dual_rail'>

The Enum and its members also have the following methods:

classmethod default(*, no_bunching)

Derive the default computation space from the legacy no_bunching flag.

Return type:

ComputationSpace

classmethod coerce(value)

Normalize user-provided values (enum instances or case-insensitive strings).

Return type:

ComputationSpace

class merlin.algorithms.layer.DetectorTransform(simulation_keys, detectors, *, dtype=None, device=None, partial_measurement=False)

Bases: Module

Linear map applying per-mode detector rules to a Fock probability vector.

Args:

simulation_keys: Iterable describing the raw Fock states produced by the

simulator (as tuples or lists of integers).

detectors: One detector per optical mode. Each detector must expose the

detect() method from perceval.Detector.

dtype: Optional torch dtype for the transform matrix. Defaults to

torch.float32.

device: Optional device used to stage the transform matrix. partial_measurement: When True, only the modes whose detector entry is

not None are measured. The transform then operates on complex amplitudes and returns per-outcome dictionaries (see forward()).

forward(tensor)

Apply the detector transform.

Return type:

Tensor | list[dict[tuple[int, ...], list[tuple[Tensor, Tensor]]]]

Args:

tensor: Probability distribution (complete mode) or amplitudes

(partial measurement). The last dimension must match the simulator basis.

Returns:

• Complete mode: real probability tensor expressed in the detector basis.

• Partial mode: list indexed by remaining photon count. Each entry is a dictionary whose keys are full-length mode tuples (unmeasured modes set to None) and whose values are lists of (probability, normalized remaining-mode amplitudes) pairs – one per perfect measurement branch.

property is_identity: bool

Whether the transform reduces to the identity (ideal PNR detectors).

property output_keys: list[tuple[int, ...]]

Return the classical detection outcome keys.

property output_size: int

Number of classical outcomes produced by the detectors.

property partial_measurement: bool

Return True when the transform runs in partial measurement mode.

remaining_basis(remaining_n=None)

Return the ordered Fock-state basis for the unmeasured modes.

Return type:

list[tuple[int, ...]]

Args:

remaining_n: Optional photon count used to select a specific block.

When omitted, the method returns the concatenation of every remaining-mode basis enumerated during detector initialisation.

Returns:

List of tuples describing the photon distribution over the unmeasured modes.

row(index, *, dtype=None, device=None)

Return a single detector transform row as a dense tensor.

Return type:

Tensor

class merlin.algorithms.layer.Iterable

Bases: object

enum merlin.algorithms.layer.MeasurementStrategy(value)

Bases: Enum

Strategy for measuring quantum states or counts and possibly apply mapping to classical outputs.

Valid values are as follows:

PROBABILITIES = <MeasurementStrategy.PROBABILITIES: 'probabilities'>

MODE_EXPECTATIONS = <MeasurementStrategy.MODE_EXPECTATIONS: 'mode_expectations'>

AMPLITUDES = <MeasurementStrategy.AMPLITUDES: 'amplitudes'>

class merlin.algorithms.layer.ModGrouping(input_size, output_size)

Bases: Module

Maps tensor to a modulo grouping of its components.

This mapper groups elements of the input tensor based on their index modulo the output size. Elements with the same modulo value are summed together to produce the output.

forward(x)

Map the input tensor to the desired output_size utilizing modulo grouping.

Args:

x: Input tensor of shape (n_batch, input_size) or (input_size,)

Returns:

Grouped tensor of shape (batch_size, output_size) or (output_size,)

class merlin.algorithms.layer.OutputMapper

Bases: object

Handles mapping quantum state amplitudes or probabilities to classical outputs.

This class provides factory methods for creating different types of output mappers that convert quantum state amplitudes or probabilities to classical outputs.

static create_mapping(strategy, computation_space=ComputationSpace.FOCK, keys=None)

Create an output mapping based on the specified strategy.

Args:

strategy: The measurement mapping strategy to use no_bunching: (Only used for ModeExpectations measurement strategy) If True (default), the per-mode probability of finding at least one photon is returned.

Otherwise, it is the per-mode expected number of photons that is returned.

keys: (Only used for ModeExpectations measurement strategy) List of tuples that represent the possible quantum Fock states.

For example, keys = [(0,1,0,2), (1,0,1,0), …]

Returns:

A PyTorch module that maps the per state amplitudes or probabilities to the desired format.

Raises:

ValueError: If strategy is unknown

class merlin.algorithms.layer.PhotonLossTransform(simulation_keys, survival_probs, *, dtype=None, device=None)

Bases: Module

Linear map applying per-mode photon loss to a Fock probability vector.

Args:

simulation_keys: Iterable describing the raw Fock states produced by the

simulator (as tuples or lists of integers).

survival_probs: One survival probability per optical mode. dtype: Optional torch dtype for the transform matrix. Defaults to

torch.float32.

device: Optional device used to stage the transform matrix.

forward(distribution)

Apply the photon loss transform to a Fock probability vector.

Return type:

Tensor

Args:

distribution: A Fock probability vector as a 1D torch tensor.

Returns:

A Fock probability vector after photon loss.

property is_identity: bool

Whether the transform corresponds to perfect transmission.

property output_keys: list[tuple[int, ...]]

Classical Fock keys after photon loss.

property output_size: int

Number of classical outcomes after photon loss.

to(*args, **kwargs)

Move and/or cast the parameters and buffers.

This can be called as

to(device=None, dtype=None, non_blocking=False)

to(dtype, non_blocking=False)

to(tensor, non_blocking=False)

to(memory_format=torch.channels_last)

Its signature is similar to torch.Tensor.to(), but only accepts floating point or complex dtypes. In addition, this method will only cast the floating point or complex parameters and buffers to dtype (if given). The integral parameters and buffers will be moved device, if that is given, but with dtypes unchanged. When non_blocking is set, it tries to convert/move asynchronously with respect to the host if possible, e.g., moving CPU Tensors with pinned memory to CUDA devices.

See below for examples.

Note

This method modifies the module in-place.

Args:

device (torch.device): the desired device of the parameters

and buffers in this module

dtype (torch.dtype): the desired floating point or complex dtype of

the parameters and buffers in this module

tensor (torch.Tensor): Tensor whose dtype and device are the desired

dtype and device for all parameters and buffers in this module

memory_format (torch.memory_format): the desired memory

format for 4D parameters and buffers in this module (keyword only argument)

Returns:

Module: self

Examples:

>>> # xdoctest: +IGNORE_WANT("non-deterministic")
>>> linear = nn.Linear(2, 2)
>>> linear.weight
Parameter containing:
tensor([[ 0.1913, -0.3420],
        [-0.5113, -0.2325]])
>>> linear.to(torch.double)
Linear(in_features=2, out_features=2, bias=True)
>>> linear.weight
Parameter containing:
tensor([[ 0.1913, -0.3420],
        [-0.5113, -0.2325]], dtype=torch.float64)
>>> # xdoctest: +REQUIRES(env:TORCH_DOCTEST_CUDA1)
>>> gpu1 = torch.device("cuda:1")
>>> linear.to(gpu1, dtype=torch.half, non_blocking=True)
Linear(in_features=2, out_features=2, bias=True)
>>> linear.weight
Parameter containing:
tensor([[ 0.1914, -0.3420],
        [-0.5112, -0.2324]], dtype=torch.float16, device='cuda:1')
>>> cpu = torch.device("cpu")
>>> linear.to(cpu)
Linear(in_features=2, out_features=2, bias=True)
>>> linear.weight
Parameter containing:
tensor([[ 0.1914, -0.3420],
        [-0.5112, -0.2324]], dtype=torch.float16)

>>> linear = nn.Linear(2, 2, bias=None).to(torch.cdouble)
>>> linear.weight
Parameter containing:
tensor([[ 0.3741+0.j,  0.2382+0.j],
        [ 0.5593+0.j, -0.4443+0.j]], dtype=torch.complex128)
>>> linear(torch.ones(3, 2, dtype=torch.cdouble))
tensor([[0.6122+0.j, 0.1150+0.j],
        [0.6122+0.j, 0.1150+0.j],
        [0.6122+0.j, 0.1150+0.j]], dtype=torch.complex128)

class merlin.algorithms.layer.QuantumLayer(input_size=None, builder=None, circuit=None, experiment=None, input_state=None, n_photons=None, trainable_parameters=None, input_parameters=None, amplitude_encoding=False, computation_space=None, measurement_strategy=MeasurementStrategy.PROBABILITIES, device=None, dtype=None, **kwargs)

Bases: Module

Enhanced Quantum Neural Network Layer with factory-based architecture.

This layer can be created either from a CircuitBuilder instance or a pre-compiled pcvl.Circuit.

Merlin integration (optimal design):

• merlin_leaf = True marks this module as an indivisible execution leaf.

• force_simulation (bool) defaults to False. When True, the layer MUST run locally.

• supports_offload() reports whether remote offload is possible (via export_config()).

• should_offload(processor, shots) encapsulates the current offload policy:

  return supports_offload() and not force_local

angle_encoding_specs: dict[str, dict[str, Any]]

as_simulation()

Temporarily force local simulation within the context.

experiment: pcvl.Experiment | None

export_config()

Export a standalone configuration for remote execution.

Return type:

dict

property force_local: bool

When True, this layer must run locally (Merlin will not offload it).

forward(*input_parameters, shots=None, sampling_method=None, simultaneous_processes=None)

Forward pass through the quantum layer.

When self.amplitude_encoding is True the first positional argument must contain the amplitude-encoded input state (either [num_states] or [batch_size, num_states]). Remaining positional arguments are treated as classical inputs and processed via the standard encoding pipeline.

Return type:

tuple[Tensor, Tensor] | Tensor

Sampling is controlled by:

• shots (int): number of samples; if 0 or None, return exact amplitudes/probabilities.

• sampling_method (str): e.g. “multinomial”.

get_experiment()

Return type:

Optional[Experiment]

property has_custom_detectors: bool

input_parameters: list[str]

merlin_leaf: bool = True

noise_model: Any | None

property output_keys

Return the Fock basis associated with the layer outputs.

property output_size: int

prepare_parameters(input_parameters)

Prepare parameter list for circuit evaluation.

Return type:

list[Tensor]

set_force_simulation(value)

Return type:

None

set_input_state(input_state)

set_sampling_config(shots=None, method=None)

Deprecated: sampling configuration must be provided at call time in forward.

should_offload(_processor=None, _shots=None)

Return True if this layer should be offloaded under current policy.

Return type:

bool

classmethod simple(input_size, n_params=90, output_size=None, device=None, dtype=None, no_bunching=True, **kwargs)

Create a ready-to-train layer with a 10-mode, 5-photon architecture.

The circuit is assembled via CircuitBuilder with the following layout:

1. A fully trainable entangling layer acting on all modes;

2. A full input encoding layer spanning all encoded features;

3. A non-trainable entangling layer that redistributes encoded information;

4. Optional trainable Mach-Zehnder blocks (two parameters each) to reach the requested n_params budget;

5. A final entangling layer prior to measurement.

Args:

input_size: Size of the classical input vector. n_params: Number of trainable parameters to allocate across the additional MZI blocks. Values

below the default entangling budget trigger a warning; values above it must differ by an even amount because each added MZI exposes two parameters.

output_size: Optional classical output width. device: Optional target device for tensors. dtype: Optional tensor dtype. no_bunching: Whether to restrict to states without photon bunching.

Returns:

QuantumLayer configured with the described architecture.

supports_offload()

Return True if this layer is technically offloadable.

Return type:

bool

to(*args, **kwargs)

Move and/or cast the parameters and buffers.

This can be called as

to(device=None, dtype=None, non_blocking=False)

to(dtype, non_blocking=False)

to(tensor, non_blocking=False)

to(memory_format=torch.channels_last)

Its signature is similar to torch.Tensor.to(), but only accepts floating point or complex dtypes. In addition, this method will only cast the floating point or complex parameters and buffers to dtype (if given). The integral parameters and buffers will be moved device, if that is given, but with dtypes unchanged. When non_blocking is set, it tries to convert/move asynchronously with respect to the host if possible, e.g., moving CPU Tensors with pinned memory to CUDA devices.

See below for examples.

Note

This method modifies the module in-place.

Args:

device (torch.device): the desired device of the parameters

and buffers in this module

dtype (torch.dtype): the desired floating point or complex dtype of

the parameters and buffers in this module

tensor (torch.Tensor): Tensor whose dtype and device are the desired

dtype and device for all parameters and buffers in this module

memory_format (torch.memory_format): the desired memory

format for 4D parameters and buffers in this module (keyword only argument)

Returns:

Module: self

Examples:

>>> # xdoctest: +IGNORE_WANT("non-deterministic")
>>> linear = nn.Linear(2, 2)
>>> linear.weight
Parameter containing:
tensor([[ 0.1913, -0.3420],
        [-0.5113, -0.2325]])
>>> linear.to(torch.double)
Linear(in_features=2, out_features=2, bias=True)
>>> linear.weight
Parameter containing:
tensor([[ 0.1913, -0.3420],
        [-0.5113, -0.2325]], dtype=torch.float64)
>>> # xdoctest: +REQUIRES(env:TORCH_DOCTEST_CUDA1)
>>> gpu1 = torch.device("cuda:1")
>>> linear.to(gpu1, dtype=torch.half, non_blocking=True)
Linear(in_features=2, out_features=2, bias=True)
>>> linear.weight
Parameter containing:
tensor([[ 0.1914, -0.3420],
        [-0.5112, -0.2324]], dtype=torch.float16, device='cuda:1')
>>> cpu = torch.device("cpu")
>>> linear.to(cpu)
Linear(in_features=2, out_features=2, bias=True)
>>> linear.weight
Parameter containing:
tensor([[ 0.1914, -0.3420],
        [-0.5112, -0.2324]], dtype=torch.float16)

>>> linear = nn.Linear(2, 2, bias=None).to(torch.cdouble)
>>> linear.weight
Parameter containing:
tensor([[ 0.3741+0.j,  0.2382+0.j],
        [ 0.5593+0.j, -0.4443+0.j]], dtype=torch.complex128)
>>> linear(torch.ones(3, 2, dtype=torch.cdouble))
tensor([[0.6122+0.j, 0.1150+0.j],
        [0.6122+0.j, 0.1150+0.j],
        [0.6122+0.j, 0.1150+0.j]], dtype=torch.complex128)

trainable_parameters: list[str]

training: bool

class merlin.algorithms.layer.Sequence

Bases: Reversible, Collection

All the operations on a read-only sequence.

Concrete subclasses must override __new__ or __init__, __getitem__, and __len__.

count(value) → integer -- return number of occurrences of value

index(value[, start[, stop]]) → integer -- return first index of value.

Raises ValueError if the value is not present.

Supporting start and stop arguments is optional, but recommended.

class merlin.algorithms.layer.StateGenerator

Bases: object

Utility class for generating photonic input states.

static generate_state(n_modes, n_photons, state_pattern)

Generate an input state based on specified pattern.

enum merlin.algorithms.layer.StatePattern(value)

Bases: Enum

Input photon state patterns.

Valid values are as follows:

DEFAULT = <StatePattern.DEFAULT: 'default'>

SPACED = <StatePattern.SPACED: 'spaced'>

SEQUENTIAL = <StatePattern.SEQUENTIAL: 'sequential'>

PERIODIC = <StatePattern.PERIODIC: 'periodic'>

merlin.algorithms.layer.cast(typ, val)

Cast a value to a type.

This returns the value unchanged. To the type checker this signals that the return value has the designated type, but at runtime we intentionally don’t check anything (we want this to be as fast as possible).

merlin.algorithms.layer.complex_dtype_for(dtype_like)

Return the matching complex dtype for the provided float or complex dtype.

Return type:

dtype

Args:

dtype_like: Representation of a torch dtype (string, numpy dtype, torch dtype, …).

Returns:

torch complex dtype corresponding to the provided representation.

Raises:

TypeError: If the dtype cannot be mapped to a supported float/complex pair.

merlin.algorithms.layer.contextmanager(func)

@contextmanager decorator.

Typical usage:

@contextmanager def some_generator(<arguments>):

<setup> try:

yield <value>

finally:

<cleanup>

This makes this:

with some_generator(<arguments>) as <variable>:

<body>

equivalent to this:

<setup> try:

<variable> = <value> <body>

finally:

<cleanup>

merlin.algorithms.layer.pcvl_to_tensor(state_vector, computation_space=ComputationSpace.FOCK, dtype=torch.complex64, device=device(type='cpu'))

Convert a Perceval StateVector into a torch Tensor.

Return type:

Tensor

Args:

state_vector: Perceval StateVector. computation_space: Computation space of the state vector following combinadics ordering. dtype: Desired torch dtype of the output Tensor. device: Desired torch device of the output Tensor.

Returns:

Equivalent torch Tensor.

Raises:

ValueError: If the StateVector includes states with incompatible photon number for the specified computation space,

or non consistent number of photons across the states.

merlin.algorithms.layer.resolve_detectors(experiment, n_modes)

Build a per-mode detector list from a Perceval experiment.

Return type:

tuple[list[Detector], bool]

Args:

experiment: Perceval experiment carrying detector configuration. n_modes: Number of photonic modes to cover.

Returns:

normalized: list[pcvl.Detector]

List of detectors (defaulting to ideal PNR where unspecified),

empty_detectors: bool

If True, no Detector was defined in experiment. If False, at least one Detector was defined in experiement.

merlin.algorithms.layer.resolve_photon_loss(experiment, n_modes)

Resolve photon loss from the experiment’s noise model.

Return type:

tuple[list[float], bool]

Args:

experiment: The quantum experiment carrying the noise model. n_modes: Number of photonic modes to cover.

Returns:

Tuple containing the per-mode survival probabilities and a flag indicating whether an effective noise model was provided.

Note

Quantum layers built from a perceval.Experiment now apply the experiment’s per-mode detector configuration before returning classical outputs. When no detectors are specified, ideal photon-number resolving detectors are used by default.

If the experiment carries a perceval.NoiseModel (via experiment.noise), MerLin inserts a PhotonLossTransform ahead of any detector transform. The resulting output_keys and output_size therefore include every survival/loss configuration implied by the model, and amplitude read-out is disabled whenever custom detectors or photon loss are present.

Example: Quickstart QuantumLayer

import torch.nn as nn
from merlin import QuantumLayer

simple_layer = QuantumLayer.simple(
    input_size=4,
    n_params=120,
)

model = nn.Sequential(
    simple_layer,
    nn.Linear(simple_layer.output_size, 3),
)
# Train and evaluate as a standard torch.nn.Module

Note

QuantumLayer.simple() returns a thin SimpleSequential wrapper that behaves like a standard PyTorch module while exposing the inner quantum layer as .quantum_layer and any post-processing (ModGrouping or Identity) as .post_processing. The wrapper also forwards .circuit and .output_size so existing code that inspects these attributes continues to work.

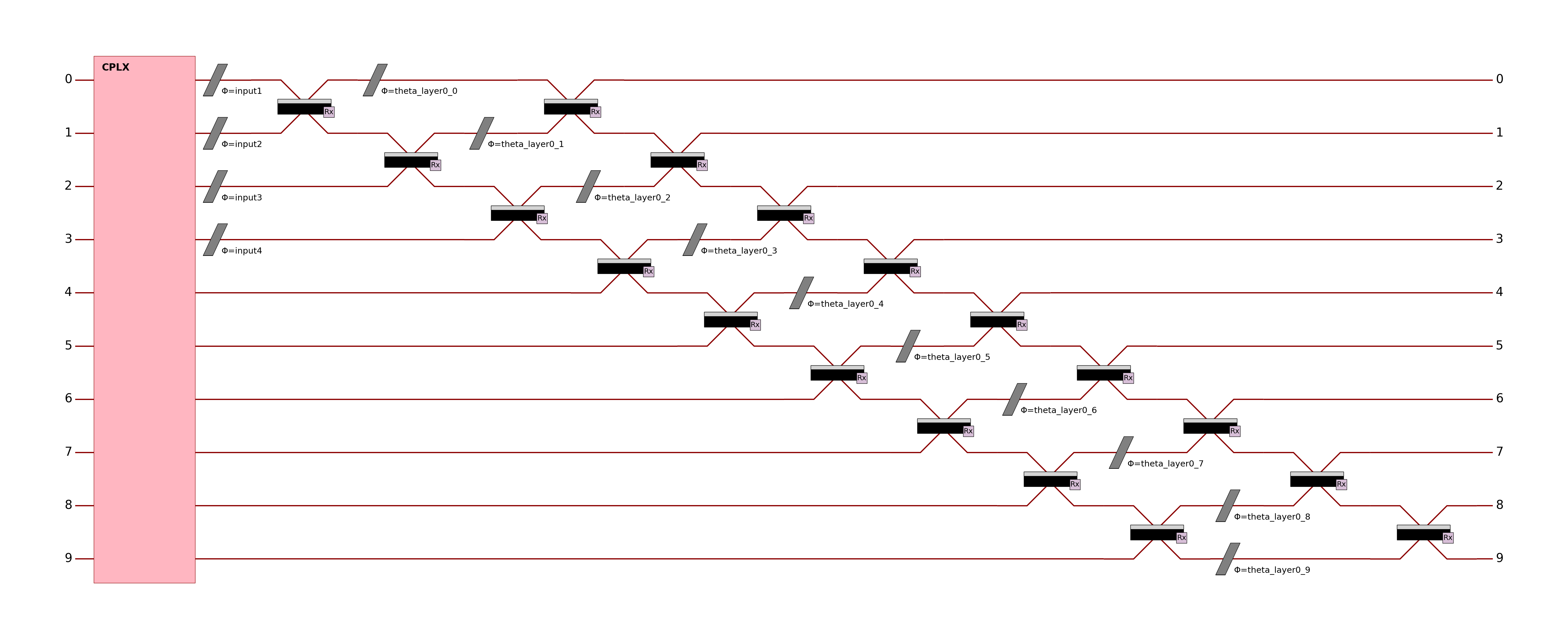
The simple quantum layer above implements a circuit of 10 modes and 5 photons with at least 90 trainable parameters. This circuit is made of: - A first entangling layer (trainable) - Angle encoding on the first N modes (for N input parameters with input_size <= n_modes) - Add MZI blocks (two trainable parameters each) to match the requested number of trainable parameters

Additional trainable budget must therefore increase in multiples of two beyond the base interferometer (90 parameters).

Example: Declarative builder API

import torch.nn as nn
from merlin import LexGrouping, MeasurementStrategy, QuantumLayer
from merlin.builder import CircuitBuilder
builder = CircuitBuilder(n_modes=6)
builder.add_entangling_layer(trainable=True, name="U1")
builder.add_angle_encoding(modes=list(range(4)), name="input")
builder.add_rotations(trainable=True, name="theta")
builder.add_superpositions(depth=1)

builder_layer = QuantumLayer(
    input_size=4,
    builder=builder,
    n_photons=3,  # is equivalent to input_state=[1,1,1,0,0,0]
    measurement_strategy=MeasurementStrategy.PROBABILITIES,
)

model = nn.Sequential(
    builder_layer,
    LexGrouping(builder_layer.output_size, 3),
)
# Train and evaluate as a standard torch.nn.Module

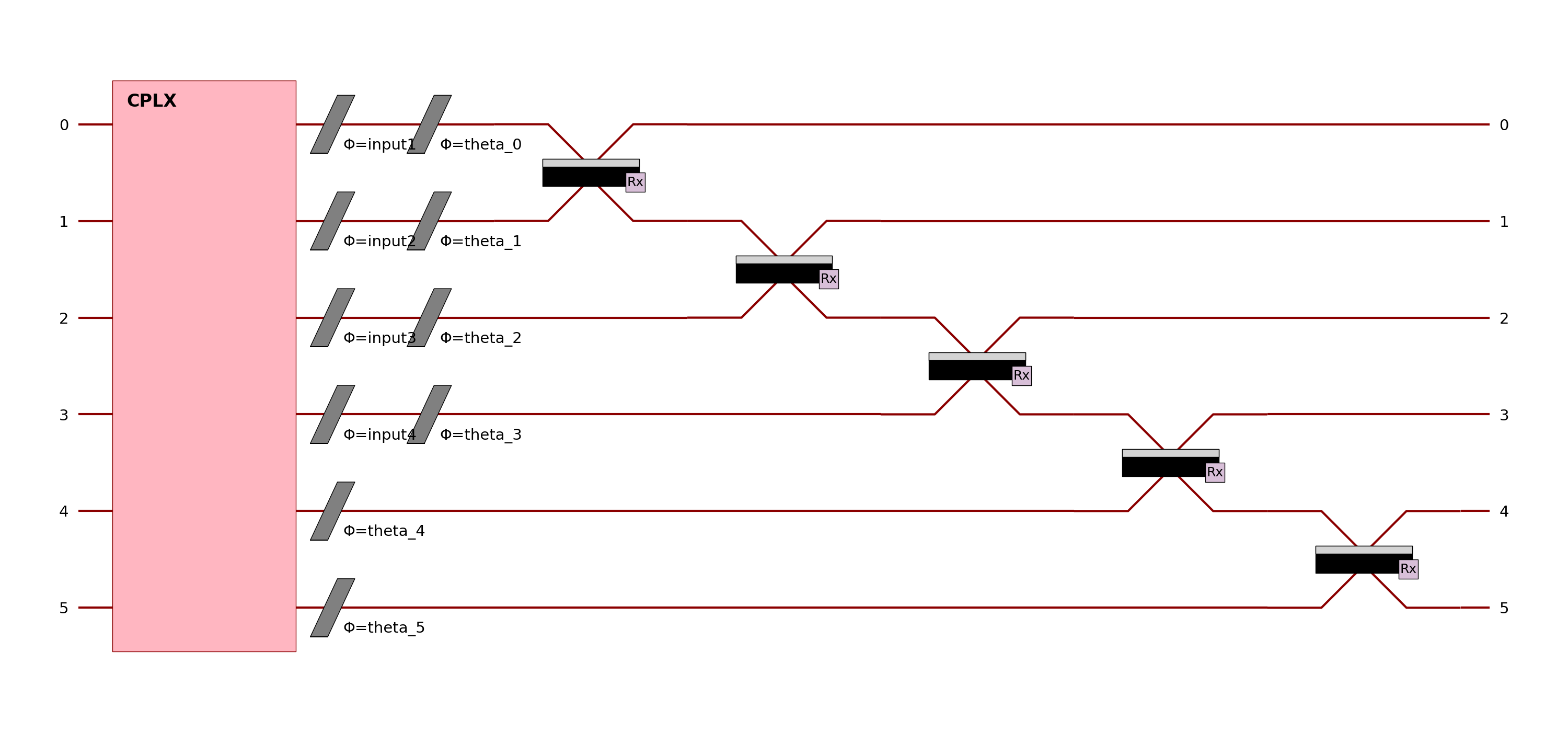
The circuit builder allows you to build your circuit layer by layer, with a high-level API. The example above implements a circuit of 6 modes and 3 photons. This circuit is made of: - A first entangling layer (trainable) - Angle encoding on the first 4 modes (for 4 input parameters with the name “input”) - A trainable rotation layer to add more trainable parameters - An entangling layer to add more expressivity

Other building blocks in the CircuitBuilder include:

• add_rotations: Add single or multiple phase shifters (rotations) to specific modes. Rotations can be fixed, trainable, or data-driven (input-encoded).

• add_angle_encoding: Encode classical data as quantum rotation angles, supporting higher-order feature combinations for expressive input encoding.

• add_entangling_layer: Insert a multi-mode entangling layer (implemented via a generic interferometer), optionally trainable, and tune its internal template with the model argument ("mzi" or "bell") for different mixing behaviours.

• add_superpositions: Add one or more beam splitters (superposition layers) with configurable targets, depth, and trainability.

Example: Manual Perceval circuit (more control)

import torch.nn as nn
import perceval as pcvl
from merlin import LexGrouping, MeasurementStrategy, QuantumLayer
modes = 6
wl = pcvl.GenericInterferometer(
    modes,
    lambda i: pcvl.BS() // pcvl.PS(pcvl.P(f"theta_li{i}")) //
    pcvl.BS() // pcvl.PS(pcvl.P(f"theta_lo{i}")),
    shape=pcvl.InterferometerShape.RECTANGLE,
)
circuit = pcvl.Circuit(modes)
circuit.add(0, wl)
for mode in range(4):
    circuit.add(mode, pcvl.PS(pcvl.P(f"input{mode}")))
wr = pcvl.GenericInterferometer(
    modes,
    lambda i: pcvl.BS() // pcvl.PS(pcvl.P(f"theta_ri{i}")) //
    pcvl.BS() // pcvl.PS(pcvl.P(f"theta_ro{i}")),
    shape=pcvl.InterferometerShape.RECTANGLE,
)
circuit.add(0, wr)

manual_layer = QuantumLayer(
    input_size=4,  # matches the number of phase shifters named "input{mode}"
    circuit=circuit,
    input_state=[1, 0, 1, 0, 1, 0],
    trainable_parameters=["theta"],
    input_parameters=["input"],
    measurement_strategy=MeasurementStrategy.PROBABILITIES,
)

model = nn.Sequential(
    manual_layer,
    LexGrouping(manual_layer.output_size, 3),
)
# Train and evaluate as a standard torch.nn.Module

See the User guide and Notebooks for more advanced usage and training routines !

Input states and amplitude encoding

The input state of a photonic circuit specifies how the photons enter the device. Physically this can be a single Fock state (a precise configuration of n_photons over m modes) or a superposed/entangled state within the same computation space (for example Bell pairs or GHZ states). QuantumLayer accepts the following representations:

• perceval.BasicState – a single configuration such as pcvl.BasicState([1, 0, 1, 0]);

• perceval.StateVector – an arbitrary superposition of basic states with complex amplitudes;

• Deprecated: Python lists, e.g. [1, 0, 1, 0]. Lists are still recognised for backward compatibility but are immediately converted to their Perceval counterparts—new code should build explicit BasicState objects.

When input_state is passed, the layer always injects that photonic state. In more elaborate pipelines you may want to cascade circuits and let the output amplitudes of the previous layer become the input state of the next. Merlin calls this amplitude encoding: the probability amplitudes themselves carry information and are passed to the next layer as a tensor. Enabling this behaviour is done with amplitude_encoding=True; in that mode the forward input of QuantumLayer is the complex photonic state.

The snippet below prepares a dual-rail Bell state as the initial condition and evaluates a batch of classical parameters:

import torch
import perceval as pcvl
from merlin.algorithms.layer import QuantumLayer
from merlin.core import ComputationSpace
from merlin.measurement.strategies import MeasurementStrategy

circuit = pcvl.Unitary(pcvl.Matrix.random_unitary(4))  # some haar-random 4-mode circuit

bell = pcvl.StateVector()
bell += pcvl.BasicState([1, 0, 1, 0])
bell += pcvl.BasicState([0, 1, 0, 1])
print(bell) # bell is a state vector of 2 photons in 4 modes

layer = QuantumLayer(
    circuit=circuit,
    n_photons=2,
    input_state=bell,
    measurement_strategy=MeasurementStrategy.PROBABILITIES,
    computation_space=ComputationSpace.DUAL_RAIL,
)

x = torch.rand(10, circuit.m)  # batch of classical parameters
amplitudes = layer(x)
assert amplitudes.shape == (10, 2**2)

For comparison, the amplitude_encoding variant supplies the photonic state during the forward pass:

import torch
import perceval as pcvl
from merlin.algorithms.layer import QuantumLayer
from merlin.core import ComputationSpace

circuit = pcvl.Circuit(3)

layer = QuantumLayer(
    circuit=circuit,
    n_photons=2,
    amplitude_encoding=True,
    computation_space=ComputationSpace.UNBUNCHED,
    dtype=torch.cdouble,
)

prepared_states = torch.tensor(
    [[1.0 + 0.0j, 0.0 + 0.0j, 0.0 + 0.0j],
     [0.0 + 0.0j, 0.0 + 0.0j, 1.0 + 0.0j]],
    dtype=torch.cdouble,
)

out = layer(prepared_states)

In the first example the circuit always starts from bell; in the second, each row of prepared_states represents a different logical photonic state that flows through the layer. This separation allows you to mix classical angle encoding with fully quantum, amplitude-based data pipelines.