Quantum Bridge: Advanced Guide and Theory
This guide explains the internal workings of the Quantum Bridge for advanced users who want to understand the QLOQ (Qubit Logic on Qudits) encoding scheme and customize their qubit-to-photonic mappings.
Theory and Architecture
QLOQ: One-Hot Encoding for Photonics
The Quantum Bridge implements the Qubit Logic on Qudits (QLOQ) encoding from Lysaght et al., which uses a one-hot encoding scheme to map groups of qubits to photonic Fock states. Each group of qubits is encoded using exactly one photon distributed across multiple modes.
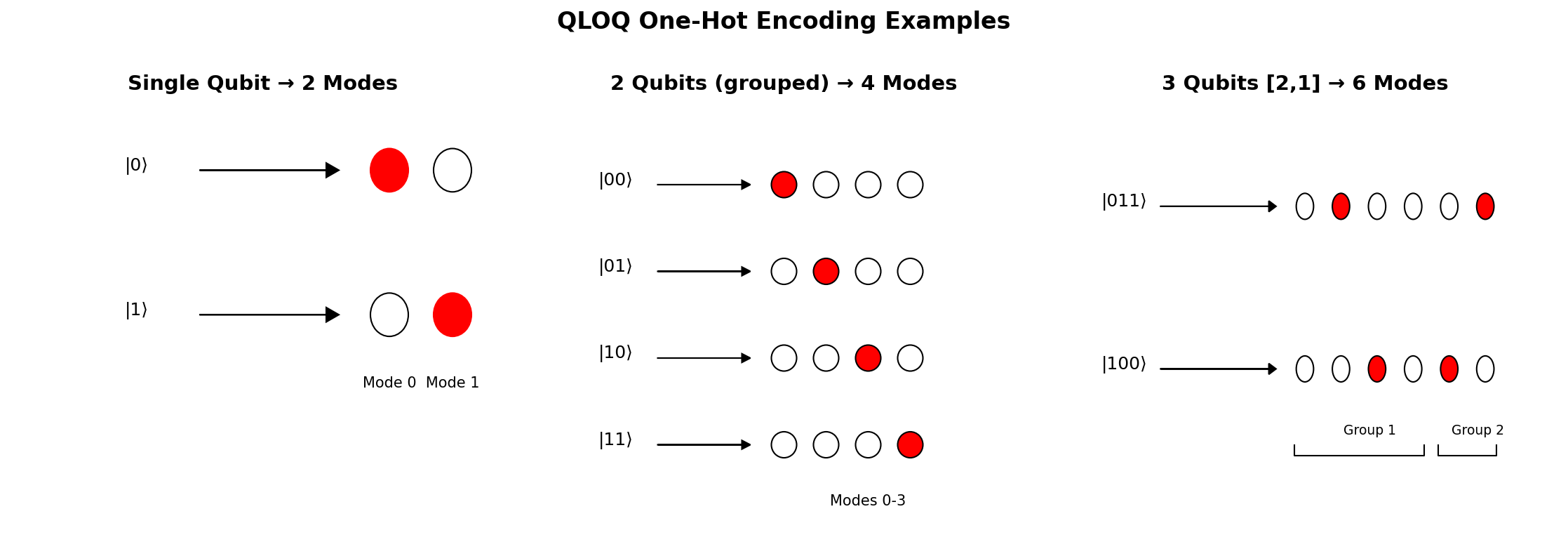
Figure: One-hot encoding examples for different qubit groupings. Red circles represent photons, white circles are empty modes.
One-Hot Encoding Principle
For a group of k qubits, we have 2^k possible basis states. Each basis state is mapped to exactly one photon in one of 2^k modes:
Qubit state |i> --> Photonic state with 1 photon at position i
Example for 2 qubits (4 basis states, 4 modes):
Qubit Binary Decimal Photonic (one-hot)
|00> 00 0 |1000>
|01> 01 1 |0100>
|10> 10 2 |0010>
|11> 11 3 |0001>
This is a one-hot encoding where the position of the single photon encodes the qubit basis state.
Example: Single Qubit to Two Modes
A single qubit has 2 basis states, mapped to 2 photonic modes with 1 photon:
Single Qubit Mapping
====================
Qubit space Photonic space
----------- --------------
|0> --> |10>
(photon in mode 0)
|1> --> |01>
(photon in mode 1)
Superposition example:
----------------------
Input: (1/sqrt(2))|0> + (1/sqrt(2))|1>
Output: (1/sqrt(2))|10> + (1/sqrt(2))|01>
import torch
from merlin.bridge import QuantumBridge
# Create bridge for 1 qubit
bridge = QuantumBridge(n_photons=1, n_modes=2)
# Qubit amplitudes for equal superposition
qubit_state = torch.tensor([0.707, 0.707], dtype=torch.complex64)
# Convert to photonic
photonic_state = bridge(qubit_state)
# Result: [0.707, 0.707] in Fock basis {|10>, |01>}
Example: Two Qubits to Four Modes
Two qubits encoded together have 4 basis states, mapped to 4 modes with 1 photon:
Two-Qubit Mapping (Single Group)
=================================
Qubit states Photonic states
------------ ---------------
|00> (idx 0) --> |1000> (photon in mode 0)
|01> (idx 1) --> |0100> (photon in mode 1)
|10> (idx 2) --> |0010> (photon in mode 2)
|11> (idx 3) --> |0001> (photon in mode 3)
Bell State Example:
-------------------
Input: (1/sqrt(2))|00> + (1/sqrt(2))|11>
Output: (1/sqrt(2))|1000> + (1/sqrt(2))|0001>
bridge = QuantumBridge(
n_photons=1,
n_modes=4,
qubit_groups=[2] # 2 qubits in one group
)
# Bell state
bell_state = torch.zeros(4, dtype=torch.complex64)
bell_state[0] = 0.707 # |00>
bell_state[3] = 0.707 # |11>
photonic_state = bridge(bell_state)
# Photonic amplitudes: 0.707 at |1000> and 0.707 at |0001>
Example: Mixed Grouping
When qubits are in different groups, each group gets its own one-hot encoded photon:
3 Qubits with [2,1] Grouping
=============================
Group 1: Qubits 0,1 (4 modes, 1 photon)
Group 2: Qubit 2 (2 modes, 1 photon)
Total: 6 modes, 2 photons
Mapping with wires_order="little" (default):
---------------------------------------------
Note: In little-endian, |abc> means qubit 0=c, qubit 1=b, qubit 2=a
Qubit state |abc> --> Photonic state
|000> = |00>|0> --> |1000|10> = |100010>
|001> = |10>|0> --> |0010|10> = |001010>
|010> = |01>|0> --> |0100|10> = |010010>
|011> = |11>|0> --> |0001|10> = |000110>
|100> = |00>|1> --> |1000|01> = |100001>
|101> = |10>|1> --> |0010|01> = |001001>
|110> = |01>|1> --> |0100|01> = |010001>
|111> = |11>|1> --> |0001|01> = |000101>
First 4 modes encode qubits 0,1 (as a group)
Last 2 modes encode qubit 2
bridge = QuantumBridge(
n_photons=2,
n_modes=6,
qubit_groups=[2, 1]
)
# Example: |011> state
state_011 = torch.zeros(8, dtype=torch.complex64)
state_011[3] = 1.0 # Binary 011 = decimal 3
photonic = bridge(state_011)
# Creates |000110> in the 2-photon Fock space
Complete Amplitude Mapping Example

Amplitude preservation in the QLOQ mapping - each qubit amplitude maps to exactly one photonic state.
Here’s how a general quantum state’s amplitudes transfer to the photonic encoding:
Amplitude Preservation in QLOQ
===============================
3-qubit quantum state with arbitrary amplitudes (wires_order="little"):
Qubit State Amplitude Maps to Photonic State
----------- --------- ----------------------
|000> a0 |100010> (gets amplitude a0)
|001> a1 |001010> (gets amplitude a1)
|010> a2 |010010> (gets amplitude a2)
|011> a3 |000110> (gets amplitude a3)
|100> a4 |100001> (gets amplitude a4)
|101> a5 |001001> (gets amplitude a5)
|110> a6 |010001> (gets amplitude a6)
|111> a7 |000101> (gets amplitude a7)
Key Property: Every amplitude is preserved exactly!
Note: With little-endian ordering, |abc> means qubit 0=c, qubit 1=b, qubit 2=a
import torch
import numpy as np
from merlin.bridge import QuantumBridge
# 3-qubit state with random amplitudes
n_qubits = 3
qubit_amps = torch.randn(8, dtype=torch.complex64)
qubit_amps = qubit_amps / torch.norm(qubit_amps)
print("Qubit amplitudes:")
for i in range(8):
binary = format(i, '03b')
print(f" |{binary}>: {qubit_amps[i]:.3f}")
# Map to photonic with [2, 1] grouping
bridge = QuantumBridge(
n_photons=2,
n_modes=6,
qubit_groups=[2, 1]
)
photonic_amps = bridge(qubit_amps)
# Verify amplitude preservation
for i in range(8):
binary = format(i, '03b')
fock_state = bridge.qubit_to_fock_state(binary)
print(f"|{binary}> -> {fock_state}")
Understanding the Transition Matrix
The transition matrix implements this one-hot mapping:
Transition Matrix Structure (Example: 2 qubits, dual-rail)
===========================================================
Photonic \ Qubit |00> |01> |10> |11>
---------------- --- --- --- ---
|1010> 1 0 0 0
|1001> 0 1 0 0
|0110> 0 0 1 0
|0101> 0 0 0 1
(other states) 0 0 0 0
Properties:
- Exactly one "1" per column (one-hot)
- Very sparse (only 2^n non-zeros out of C(m,p) x 2^n entries)
- Preserves unitarity of quantum operations
def visualize_transition_matrix(bridge):
"""Show the one-hot structure of the transition matrix."""
T = bridge.transition_matrix()
# For small examples, convert to dense
if bridge.n_qubits <= 3:
T_dense = T.to_dense().real.numpy()
# Print structure
print("Transition Matrix Structure:")
print("Each column has exactly one 1 (one-hot encoding)")
print(f"Shape: {T_dense.shape}")
# Verify one-hot property
for col in range(T_dense.shape[1]):
assert np.sum(T_dense[:, col]) == 1.0
print(f"Sparsity: {1 - T._nnz()/(T.shape[0]*T.shape[1]):.2%}")
print(f"Each qubit state maps to exactly one Fock state")
Custom Encoding Schemes
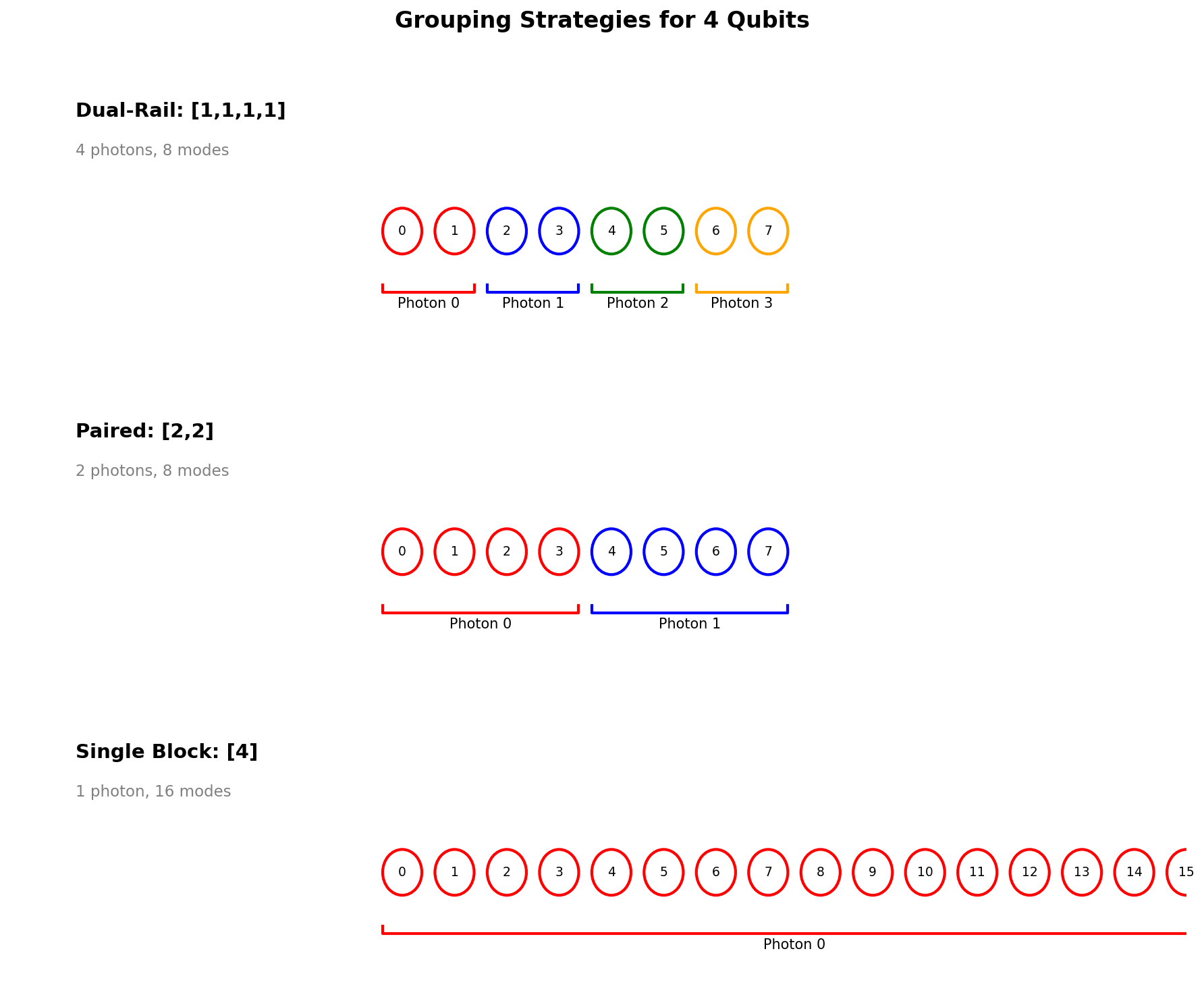
Different grouping strategies for 4 qubits showing photon and mode distribution.
Understanding qubit_groups
The qubit_groups parameter controls how qubits are partitioned for one-hot encoding:
# Example: 5 qubits with mixed grouping
qubit_groups = [3, 1, 1]
# Interpretation:
# - Qubits 0,1,2: one-hot encoded with 1 photon across 8 modes
# - Qubit 3: one-hot encoded with 1 photon across 2 modes
# - Qubit 4: one-hot encoded with 1 photon across 2 modes
# Total: 3 photons, 12 modes
Designing Custom Encodings
Consider these factors when designing custom encodings:
Entanglement Structure
Groups preserve internal entanglement but limit cross-group operations:
# For algorithms with natural 2-qubit gates
# Group pairs that interact frequently
qubit_groups = [2, 2, 2] # 3 photons for 6 qubits
# For global entanglement patterns
# Use larger groups
qubit_groups = [4, 2] # 2 photons for 6 qubits
Resource Optimization
Fewer photons reduce circuit complexity but increase mode count:
def analyze_encoding(qubit_groups):
n_qubits = sum(qubit_groups)
n_photons = len(qubit_groups)
n_modes = sum(2**g for g in qubit_groups)
print(f"Qubits: {n_qubits}")
print(f"Photons: {n_photons}")
print(f"Modes: {n_modes}")
print(f"Photon efficiency: {n_qubits/n_photons:.2f} qubits/photon")
print(f"Mode efficiency: {n_qubits/n_modes:.2f} qubits/mode")
# Compare different 4-qubit encodings
analyze_encoding([1, 1, 1, 1]) # Dual-rail: 4 photons, 8 modes
analyze_encoding([2, 2]) # Paired: 2 photons, 8 modes
analyze_encoding([4]) # Single block: 1 photon, 16 modes
Hardware Constraints
Match encoding to photonic hardware capabilities:
# For hardware with limited photon-number resolution
# Prefer more photons, fewer modes per photon
hardware_friendly = [1, 1, 1, 1, 1, 1] # 6 photons, 12 modes
# For hardware with many modes but photon-loss
# Prefer fewer photons
loss_tolerant = [3, 3] # 2 photons, 16 modes
Internal Mechanics
Wires Order and Bit Interpretation
The wires_order parameter controls how bitstrings map to qubit indices:
# Little-endian (default): LSB = qubit 0
# |01> with wires_order="little" means:
# qubit 0 = |1>
# qubit 1 = |0>
# Big-endian: MSB = qubit 0
# |01> with wires_order="big" means:
# qubit 0 = |0>
# qubit 1 = |1>
def demonstrate_wires_order():
import torch
from merlin.bridge import QuantumBridge
state = torch.zeros(4, dtype=torch.complex64)
state[1] = 1.0 # |01> in computational basis
bridge_little = QuantumBridge(
n_photons=2, n_modes=4,
wires_order="little"
)
bridge_big = QuantumBridge(
n_photons=2, n_modes=4,
wires_order="big"
)
# Different photonic states from same input
little_fock = bridge_little.qubit_to_fock_state("01")
big_fock = bridge_big.qubit_to_fock_state("01")
print(f"Little-endian: |01> -> {little_fock}")
print(f"Big-endian: |01> -> {big_fock}")
Computation Space Enumeration
The bridge maps to different photonic spaces with varying dimensions:
from merlin.bridge import QuantumBridge, ComputationSpace
import math
def compare_spaces(n_qubits):
groups = [1] * n_qubits
n_modes = 2 * n_qubits
spaces = {
"DUAL_RAIL": ComputationSpace.DUAL_RAIL,
"UNBUNCHED": ComputationSpace.UNBUNCHED,
"FOCK": ComputationSpace.FOCK
}
for name, space in spaces.items():
try:
bridge = QuantumBridge(
n_photons=n_qubits,
n_modes=n_modes,
qubit_groups=groups,
computation_space=space
)
# Calculate theoretical size
if space == ComputationSpace.DUAL_RAIL:
theory = 2**n_qubits
elif space == ComputationSpace.UNBUNCHED:
theory = math.comb(n_modes, n_qubits)
else: # FOCK
theory = math.comb(n_modes + n_qubits - 1, n_qubits)
print(f"{name}:")
print(f" Output size: {bridge.output_size}")
print(f" Theoretical: {theory}")
print(f" Sparsity: {2**n_qubits / theory:.2%}")
except ValueError as e:
print(f"{name}: {e}")
Sparse Matrix Optimization
The transition matrix is stored as a sparse COO tensor for efficiency:
def examine_transition_matrix(bridge):
"""Analyze the sparsity structure of the transition matrix."""
T = bridge.transition_matrix()
print(f"Matrix shape: {T.shape}")
print(f"Non-zero entries: {T._nnz()}")
print(f"Sparsity: {1 - T._nnz() / (T.shape[0] * T.shape[1]):.4%}")
# The matrix has exactly 2^n_qubits non-zeros (one per basis state)
# This is optimal for the one-hot QLOQ encoding
# Convert to dense for small examples (warning: memory intensive)
if bridge.n_qubits <= 3:
T_dense = T.to_dense()
print(f"Dense matrix:\n{T_dense.real.numpy()}")
Advanced Patterns
Working with Amplitude Preservation
The one-hot encoding preserves all quantum amplitudes exactly:
import torch
from merlin.bridge import QuantumBridge
def verify_amplitude_preservation():
"""Show that all amplitudes are preserved in the mapping."""
# Create a random 3-qubit state
qubit_state = torch.randn(8, dtype=torch.complex64)
qubit_state = qubit_state / torch.norm(qubit_state)
# Try different encodings
encodings = {
"dual-rail": [1, 1, 1],
"mixed": [2, 1],
"single": [3]
}
for name, groups in encodings.items():
bridge = QuantumBridge(
n_photons=len(groups),
n_modes=sum(2**g for g in groups),
qubit_groups=groups
)
photonic_state = bridge(qubit_state)
# Check norm preservation
assert torch.allclose(
torch.norm(photonic_state),
torch.norm(qubit_state),
rtol=1e-5
)
print(f"{name}: Norm preserved ✓")
# The amplitudes are redistributed but preserved
# Each qubit amplitude appears exactly once in the photonic space
Dynamic Encoding Selection
Choose encoding based on circuit structure:
class AdaptiveEncoding:
"""Select optimal encoding based on gate connectivity."""
@staticmethod
def analyze_circuit_connectivity(gates):
"""Analyze two-qubit gate patterns."""
from collections import defaultdict
connectivity = defaultdict(set)
for gate in gates:
if len(gate.qubits) == 2:
q1, q2 = gate.qubits
connectivity[q1].add(q2)
connectivity[q2].add(q1)
return connectivity
@staticmethod
def suggest_grouping(n_qubits, connectivity):
"""Suggest qubit groups based on connectivity."""
groups = []
assigned = set()
# Group highly connected qubits
for q in range(n_qubits):
if q not in assigned:
cluster = {q}
cluster.update(connectivity.get(q, set()))
cluster = cluster - assigned
# Limit group size for practicality
if len(cluster) > 3:
cluster = set(list(cluster)[:3])
groups.append(len(cluster))
assigned.update(cluster)
return groups
Hybrid Encoding Strategies
Mix different encoding types within one circuit:
class HybridEncoder(torch.nn.Module):
"""Use different encodings for different circuit sections."""
def __init__(self):
super().__init__()
# Control qubits: individual encoding for flexibility
self.control_bridge = QuantumBridge(
n_photons=2,
n_modes=4,
qubit_groups=[1, 1]
)
# Data qubits: block encoding for efficiency
self.data_bridge = QuantumBridge(
n_photons=1,
n_modes=8,
qubit_groups=[3]
)
# Corresponding photonic circuits
self.control_circuit = self.build_control_circuit(4)
self.data_circuit = self.build_data_circuit(8)
def forward(self, control_state, data_state):
# Process different qubit registers separately
control_photonic = self.control_bridge(control_state)
data_photonic = self.data_bridge(data_state)
# Apply respective circuits
control_out = self.control_circuit(control_photonic)
data_out = self.data_circuit(data_photonic)
return control_out, data_out
Encoding-Aware Circuit Design
Design photonic circuits that exploit specific encodings:
def design_for_encoding(qubit_groups, target_operation):
"""Create photonic circuits optimized for specific encodings."""
import perceval as pcvl
n_modes = sum(2**g for g in qubit_groups)
circuit = pcvl.Circuit(n_modes)
mode_offset = 0
for group_idx, group_size in enumerate(qubit_groups):
group_modes = 2**group_size
if group_size == 1:
# Dual-rail: Use simple beam splitters
circuit.add(
mode_offset,
pcvl.BS(theta=pcvl.P(f"theta_{group_idx}"))
)
elif group_size == 2:
# 4-mode block: Use 4x4 unitary
unitary = design_4x4_unitary(target_operation)
circuit.add(mode_offset, unitary)
else:
# Larger blocks: Use interferometer
circuit.add(
mode_offset,
pcvl.GenericInterferometer(
group_modes,
lambda i: pcvl.BS() // pcvl.PS(pcvl.P(f"phi_{group_idx}_{i}"))
)
)
mode_offset += group_modes
return circuit
Performance Analysis
Benchmarking Different Encodings
import time
import torch
from merlin.bridge import QuantumBridge
def benchmark_encodings(n_qubits, n_samples=100):
"""Compare performance of different encoding schemes."""
encodings = {
"dual-rail": [1] * n_qubits,
"paired": [2] * (n_qubits // 2) + [1] * (n_qubits % 2),
"block-4": [4] * (n_qubits // 4) + [n_qubits % 4] if n_qubits % 4 else [4] * (n_qubits // 4),
"single": [n_qubits]
}
results = {}
for name, groups in encodings.items():
if 0 in groups: # Skip invalid groupings
continue
try:
# Setup
n_modes = sum(2**g for g in groups)
bridge = QuantumBridge(
n_photons=len(groups),
n_modes=n_modes,
qubit_groups=groups
)
# Create random states
states = torch.randn(n_samples, 2**n_qubits, dtype=torch.complex64)
states = states / torch.norm(states, dim=1, keepdim=True)
# Benchmark
start = time.time()
for state in states:
_ = bridge(state)
elapsed = time.time() - start
results[name] = {
"time_per_state": elapsed / n_samples,
"photons": len(groups),
"modes": n_modes,
"output_size": bridge.output_size
}
except Exception as e:
results[name] = {"error": str(e)}
return results
Memory Footprint Analysis
def analyze_memory(qubit_groups):
"""Calculate memory requirements for different components."""
import sys
n_qubits = sum(qubit_groups)
n_photons = len(qubit_groups)
n_modes = sum(2**g for g in qubit_groups)
# Transition matrix (sparse)
sparse_entries = 2**n_qubits
sparse_memory = sparse_entries * (8 + 8 + 8) # value + 2 indices
# Dense equivalent
dense_entries = math.comb(n_modes, n_photons) * 2**n_qubits
dense_memory = dense_entries * 8
# State vectors
qubit_state_memory = 2**n_qubits * 8
photonic_state_memory = math.comb(n_modes, n_photons) * 8
print(f"Encoding: {qubit_groups}")
print(f"Sparse transition matrix: {sparse_memory / 1024:.2f} KB")
print(f"Dense equivalent: {dense_memory / 1024:.2f} KB")
print(f"Memory savings: {(1 - sparse_memory/dense_memory):.1%}")
print(f"Qubit state: {qubit_state_memory / 1024:.2f} KB")
print(f"Photonic state: {photonic_state_memory / 1024:.2f} KB")
Extending the Bridge
Custom Basis Mappings
Implement alternative qubit-to-photonic mappings:
class CustomBridge(QuantumBridge):
"""Extended bridge with custom basis mapping."""
def _bitstring_to_occ_custom(self, bitstring):
"""Override to implement custom mapping logic."""
# Example: Gray code mapping
gray = int(bitstring, 2)
gray ^= (gray >> 1)
# Convert to photonic occupation
fock_state = [0] * self.n_modes
fock_state[gray % self.n_modes] = 1
return tuple(fock_state)
def _build_transition_matrix(self):
"""Build transition with custom mapping."""
# Override parent method
# Implement custom logic here
return super()._build_transition_matrix()
Integration with Quantum Compilers
class CompilerIntegration:
"""Integrate bridge with quantum circuit compilers."""
@staticmethod
def from_qasm(qasm_string):
"""Create bridge configuration from OpenQASM."""
# Parse QASM to identify qubit usage patterns
# Suggest optimal grouping
pass
@staticmethod
def to_photonic_qasm(bridge, qubit_circuit):
"""Compile qubit circuit to photonic operations."""
# Translate gates based on encoding
pass
Best Practices
Profile Before Optimizing: Test different encodings with your specific circuit structure
Consider Hardware: Match encoding to available photonic hardware constraints
Monitor Sparsity: Track the sparsity of intermediate states to detect inefficiencies
Validate Mappings: Use
qubit_to_fock_stateto verify correct basis mappingsBatch Operations: Process multiple states together for better performance
References
QLOQ Paper: Lysaght, L., Goubault, T., Sinnott, P., Mansfield, S., & Emeriau, P.-E. “Quantum circuit compression using qubit logic on qubits”